LLM训练07 张量并行

0415

分布式训练topic由以下几部分组成：

LLM训练01 分布式通信

LLM训练02 显存占用分析

LLM训练03 高效训练方法

LLM训练04 数据并行

LLM训练05 ZeRO系列

LLM训练06 流水线并行

LLM训练07 张量并行

LLM训练08 Megatron-LM 源码分析

1.矩阵切分

背景：Transformer中存在大量的线性层MLP网络:Y=X*W+b。

问题：如果W参数太大，一张GPU卡显存难以满足，可以将矩阵运算分配到不同的GPU上。

简介：将矩阵乘法运算：Y=X*W，可以进行切分成若干个小矩阵相乘，张量并行的核心就是矩阵切分。

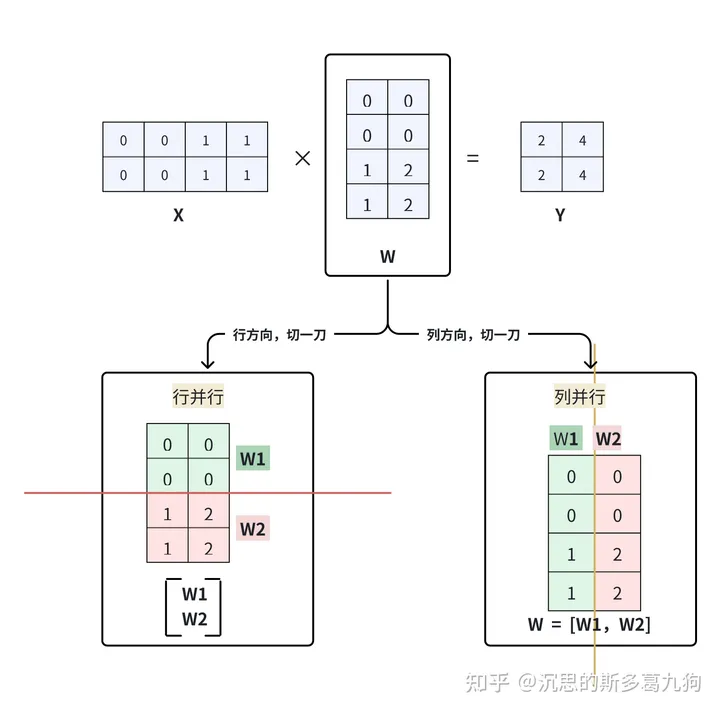
按照对权重W切分的方式，可以分为行并行和列并行，如下图所示：

  • 在Megatron-LM中，列并行，ColumnParallelLinear实现。
  • 在Megatron-LM中，行并行，RowParallelLinear实现。

IMG_256

1.1 行并行

1.1.1 原理

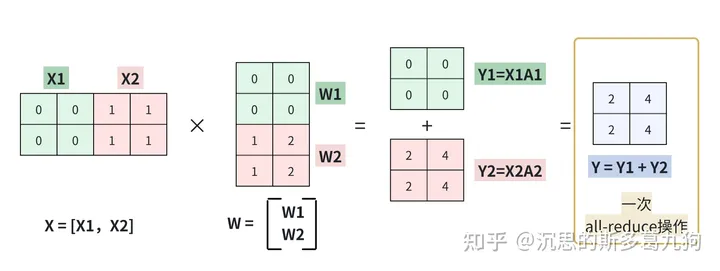
简介：在W方向，横向进行切分，切分成若干个W1,W2,…Wi。

矩阵乘法转换为以下表达：

XW=[X1,X2][W1W2]=X1W1+X2W2=Y1+Y2=Y

流程由以下三步构成：

  • step1：矩阵分割，对张量X和W分别进行分割。
  • step2：矩阵相乘，各个 Xi@ Wi

    • GPU0实现 X1和W1的矩阵相乘
    • GPU1实现 X2和W2的矩阵相乘
  • step3：结果求和， Y=Y1+Y2。计算完成，对Yi做1次all-reduce求和操作。

IMG_257

1.1.2 代码实现

import osimport torchimport torch.distributed as distimport torch.multiprocessing as mpdef run_row_parallel(rank,world_size):

group = dist.new_group(ranks=list(range(world_size)))

X = torch.tensor([[0., 0., 1., 1.], [0., 0., 1., 1.]])

A = torch.tensor([[0., 0.], [0., 0.], [1., 2.], [1., 2.]])

#1、张量X切分

X_rank = torch.split(X, 2, dim=1)[rank]

X_rank = X_rank.to(torch.device(“cuda”, rank))

#1、张量A切分

A_rank = torch.split(A, 2, dim=0)[rank]

A_rank = A_rank.to(torch.device(“cuda”, rank))

print (f”step1: 张量X切分 rank num is {rank}, X_rank:\n{X_rank} \n”)

print (f”step1: 张量A切分 rank num is {rank}, A_rank:\n{A_rank} \n”)

#2、矩阵乘法, X1A1 X2A2

input_ = X_rank@A_rank

print (f”step2: 矩阵乘法X1A1 ,rank num is {rank}, input_:\n{input_} \n”)

#3、all_reduce操作，Y=Y1+Y2

dist.all_reduce(tensor=input_,op=dist.ReduceOp.SUM,group=group)

print(f”step3: all_reduce操作，Y=Y1+Y2 rank num is {rank},input_:\n{input_} \n”)

打印结果：

step1: 张量X切分 rank num is 1, X_rank:

tensor([[1., 1.],

[1., 1.]], device=’cuda:1′)

step1: 张量A切分 rank num is 1, A_rank:

tensor([[1., 2.],

[1., 2.]], device=’cuda:1′)

step1: 张量X切分 rank num is 0, X_rank:

tensor([[0., 0.],

[0., 0.]], device=’cuda:0′)

step1: 张量A切分 rank num is 0, A_rank:

tensor([[0., 0.],

[0., 0.]], device=’cuda:0′)

step2: 矩阵乘法X1A1 ,rank num is 1, input_:

tensor([[2., 4.],

[2., 4.]], device=’cuda:1′)

step2: 矩阵乘法X1A1 ,rank num is 0, input_:

tensor([[0., 0.],

[0., 0.]], device=’cuda:0′)

step3: all_reduce操作，Y=Y1+Y2 rank num is 1,input_:

tensor([[2., 4.],

[2., 4.]], device=’cuda:1′)

step3: all_reduce操作，Y=Y1+Y2 rank num is 0,input_:

tensor([[2., 4.],

[2., 4.]], device=’cuda:0′)

1.2 列并行

1.2.1 原理

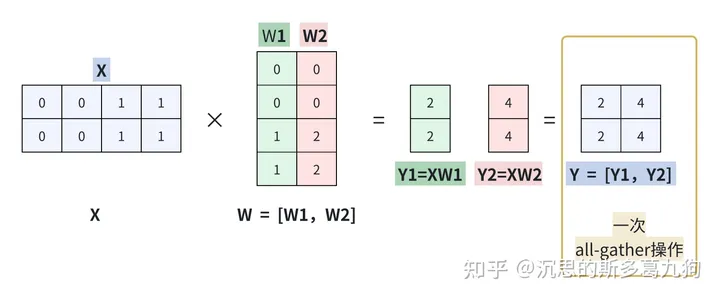
简介：在W方向，进行纵向切，切分成若干个W1,W2,…Wi。

矩阵乘法转换为以下表达：

XW=X[W1,W2]=[XW1,XW2]=[Y1,Y2]=Y

流程由以下三步构出：

  • step1：矩阵分割，只对矩阵W进行分割。
  • step2：矩阵相乘，各个 X@ Wi

    • GPU0实现 X和W1的矩阵相乘
    • GPU1实现 X和W2的矩阵相乘
  • step3：结果收集concat， Y=[Y1,Y2]。计算完成，对Yi做1次all-gather操作。

IMG_258

1.2.2 代码实现

def run_column_parallel(rank,world_size):

group = dist.new_group(ranks=list(range(world_size)))

X = torch.tensor([[0., 0., 1., 1.], [0., 0., 1., 1.]])

A = torch.tensor([[0., 0.], [0., 0.], [1., 2.], [1., 2.]])

#1、张量A切分

A_rank = torch.split(A, 1, dim=1)[rank]

A_rank = A_rank.to(torch.device(“cuda”, rank))

X = X.to(torch.device(“cuda”, rank))

print (f”step1: 张量A切分 rank num is {rank}, A_rank:\n{A_rank} \n”)

#2、矩阵乘法, XA1 XA2

input_ = X@A_rank

tensor_list = [torch.empty_like(input_) for _ in range(world_size)]

tensor_list[rank] = input_

print (f”step2: 矩阵乘法XA1 ,rank num is {rank}, input_:\n{input_} \n”)

#3、all-gather操作：Y= [Y1,Y2]

dist.all_gather(tensor_list=tensor_list, tensor=input_, group=group)

#print (f”step3: all-gather操作，Y= [Y1,Y2] ,rank num is {rank}, tensor_list:\n{tensor_list} \n”)

output = torch.cat(tensor_list,dim=1)

print (f”step3: all-gather操作，Y= [Y1,Y2] ,rank num is {rank}, output:\n{output} \n”)

打印结果如下：

step1: 张量A切分 rank num is 0, A_rank:tensor([[0.],

[0.],

[1.],

[1.]], device=‘cuda:0’)

step1: 张量A切分 rank num is 1, A_rank:tensor([[0.],

[0.],

[2.],

[2.]], device=‘cuda:1’)

step2: 矩阵乘法XA1 ,rank num is 0, input_:tensor([[2.],

[2.]], device=‘cuda:0’) step2: 矩阵乘法XA1 ,rank num is 1, input_:tensor([[4.],

[4.]], device=‘cuda:1’)

step3: all–gather操作，Y= [Y1,Y2] ,rank num is 0, output:tensor([[2., 4.],

[2., 4.]], device=‘cuda:0’) step3: all–gather操作，Y= [Y1,Y2] ,rank num is 1, output:tensor([[2., 4.],

[2., 4.]], device=‘cuda:1’)

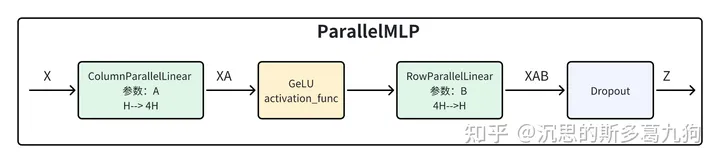
2.并行MLP

2.1 ParallelMLP介绍

2.1.1 简介

简介：Megatron-LM的并行MLP包含了两个线性层。

第一个线性层实现了 hidden size 到4 x hidden size 的转换；

第二个线性层实现了4 x hidden size 回到 hidden size；

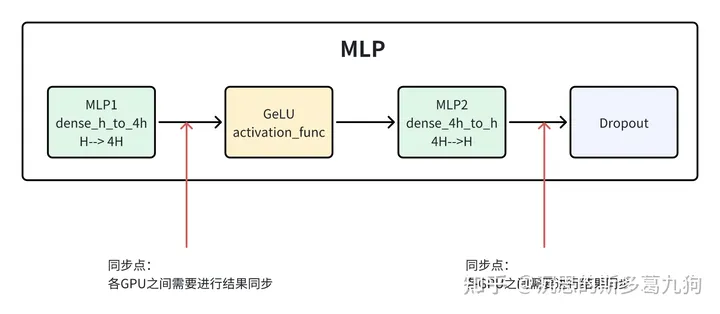
IMG_259

问题：每个线性层可以采用行并行或者列并行的方法进行拆分，2个线性层理论上可以有2*2=4种方法进行拆分。选择哪一种组合方法。

选择关键：每一次计算完成，各GPU间需要同步结果，再进行下一次计算。好的组合方式，可以减少同步点（同步结果），降低GPU之间的通信时间。

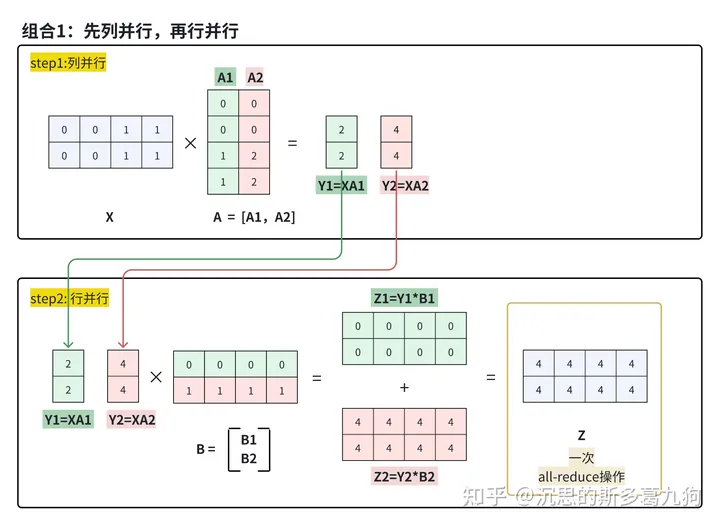
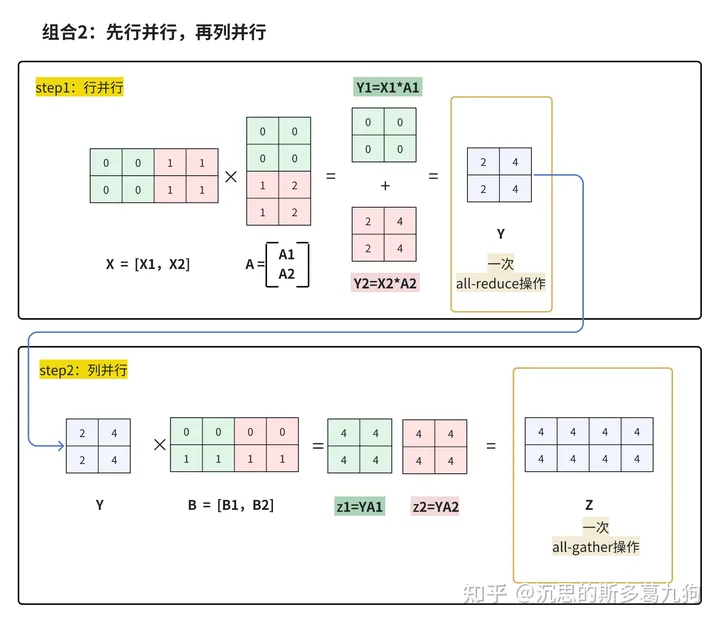
答案：Megatron-LM中采用了组合1的方法：先列并行，再行并行。

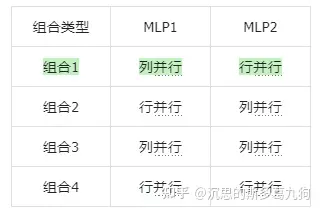
IMG_260

2.1.2 ParallelMLP实现方法对比

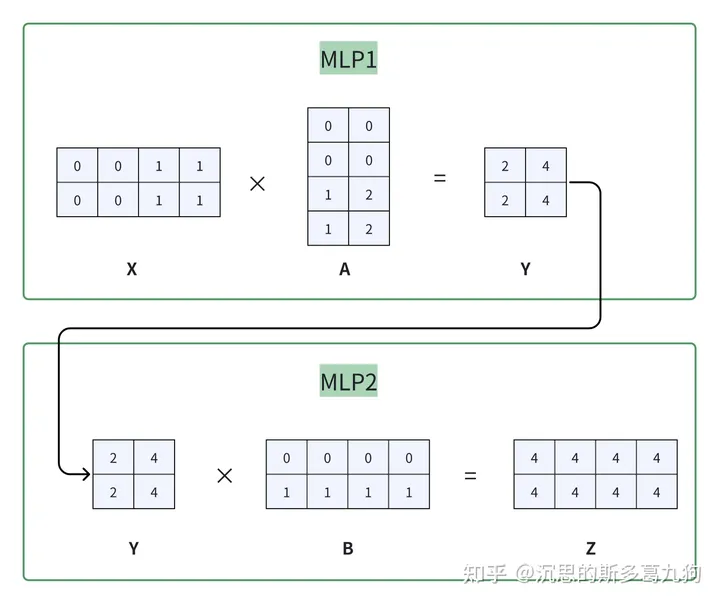
针对上文中的组合1和组合2进行对比分析：

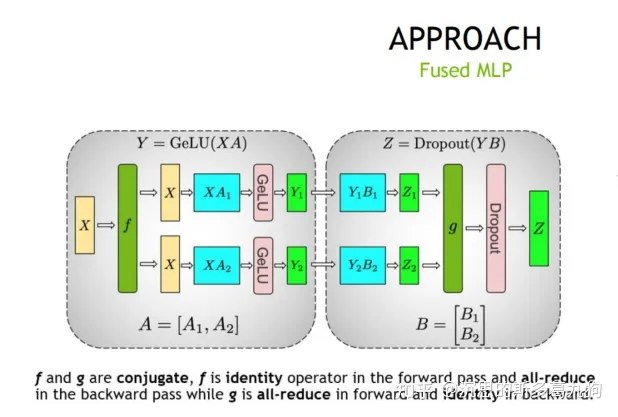
假设2个线性层分别为以下矩阵乘法，如下图所示：

  • 第1个线性层MLP1：X*A=Y
  • 第2个线性层MLP2：Y*B=Z

IMG_261

组合1：第一个MLP计算完成，不需要对结果Y进行同步，也可以直接计算第二个MLP，减少一次同步点。

IMG_262

组合2：第一个MLP计算完成，必须对结果Y进行同步，否则无法计算第二个MLP。

IMG_263

组合1代码实现：先列并行，再行并行

def run_column_row_para(rank,world_size):

#方法1：先列并行，再行并行 就是ParalleMLP实现

group = dist.new_group(ranks=list(range(world_size)))

X = torch.tensor([[0., 0., 1., 1.], [0., 0., 1., 1.]])#[2,4]

A = torch.tensor([[0., 0.], [0., 0.], [1., 2.], [1., 2.]]) #[4,2]

B = torch.tensor([[0., 0., 0., 0.], [1., 1., 1., 1.]])#[2,4]

#1、列并行，张量A切分,Y1=XA1 Y2=XA2

A_rank = torch.split(A, 1, dim=1)[rank] #[4,1]

A_rank = A_rank.to(torch.device(“cuda”, rank))

X = X.to(torch.device(“cuda”, rank))

Y_rank = X@A_rank #[2,1]

#2、行并行，矩阵乘法，Y1B1

B_rank = torch.split(B,1,dim=0)[rank] #[1,4]

B_rank = B_rank.to(torch.device(“cuda”, rank))

Z= Y_rank@B_rank #[2,4]

#3、all_reduce操作

start_time = time.time()

dist.all_reduce(tensor=Z,op=dist.ReduceOp.SUM,group=group)

end_time = time.time()

print(f”方法1 先列再行 all_reduce cost time: {end_time – start_time}s”)

#print(f”step3: all_reduce操作，Z=Z1+Z2 rank num is {rank},Z:\n{Z} \n”)

组合2代码实现：先行并行，再列并行

def run_row_column_para(rank,world_size):

# 方法2：先行并行，再列并行

group = dist.new_group(ranks=list(range(world_size)))

X = torch.tensor([[0., 0., 1., 1.], [0., 0., 1., 1.]]) # [2,4]

A = torch.tensor([[0., 0.], [0., 0.], [1., 2.], [1., 2.]]) # [4,2]

B = torch.tensor([[0., 0., 0., 0.], [1., 1., 1., 1.]]) # [2,4]

# 1、行并行，张量A切分, 张量X切分，Y1=X1A1 Y2=X2A2 ,Y=Y1+Y2

A_rank = torch.split(A, 2, dim=0)[rank] # [2,2]

A_rank = A_rank.to(torch.device(“cuda”, rank))

X_rank = torch.split(X, 2, dim=1)[rank] # [2,2]

X_rank = X_rank.to(torch.device(“cuda”, rank))

Y = X_rank @ A_rank # [2,2]

start_time = time.time()

dist.all_reduce(tensor=Y, op=dist.ReduceOp.SUM, group=group)

end_time1 = time.time()

print(f”方法2 先行再列 all_reduce cost time: {end_time1 – start_time}s”)

# 2、列并行，矩阵乘法，Y1B1

B_rank = torch.split(B, 2, dim=1)[rank] # [2,2]

B_rank = B_rank.to(torch.device(“cuda”, rank))

Z_rank = Y @ B_rank # [2,2]

#

#3、all-gather操作：Y= [Y1,Y2]

tensor_list = [torch.empty_like(Z_rank) for _ in range(world_size)]

tensor_list[rank] = Z_rank

end_time2= time.time()

dist.all_gather(tensor_list=tensor_list, tensor=Z_rank, group=group)

end_time3 = time.time()

print(f”方法2 先行再列 all_gather cost time: {end_time3 – end_time2}s”)

Z= torch.cat(tensor_list, dim=0)

# print (f”step3: all-gather操作，Z= [Z1,Z2] ,rank num is {rank}, Z:\n{Z} \n”)

2.1.3 源码解读

IMG_264

#megatron/model/transformer.pyclass ParallelMLP(MegatronModule):

def __init__(self):

…

#说明输出结果Y=XA，不需要进行all-gather操作

self.dense_h_to_4h = tensor_parallel.ColumnParallelLinear(gather_output=False)

#行并行需要对输入X也进行切分，

#说明输入已经是切分好的：Y –> Y1/Y2

self.dense_4h_to_h = tensor_parallel.RowParallelLinear(input_is_parallel=True)

…

2.1.4 通信量分析

一个ParallelMLP

  • 通信次数：2次all-reduce通信，forward时1次AllReduce，做backward时产生1次AllReduce。
  • 1次all-reduce操作，单卡通信量为2* Φ
  • 单次通信量： Φ =bs*seq_len*h，输出Z的shape为：[bs, seq_len, h]
  • 总通信量：4* Φ = 2*2* Φ

IMG_265

2.2 ColumnParallelLinear

2.2.1 原理分析

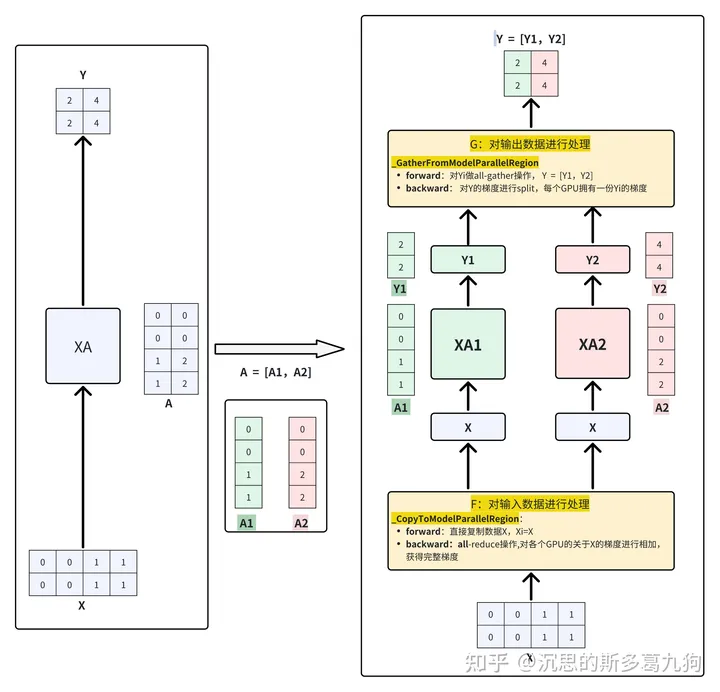
在Megatron-LM中，不能只考虑列并行矩阵乘法，还需要考虑模型的前向传播和后向传播过程，通过加入F和G算子，每个算子都包含forward和backward操作，分别对输入和输出数据进行处理，进而实现模型训练流程。

forward流程：

  • step1：通过F算子对输入数据进行处理。

    • F算子：identity 操作，把输入 X 完整的分发到每个GPU
  • step2：矩阵乘法。
  • step3：通过G算子对输出数据进行处理。

    • G算子：all-gather 操作，把输出的各个Yi进行合并，得到完整的Y。

如下图所示：

IMG_266

2.2.2 源码解读

ColumnParallelLinear的forward流程如下所示：

源码：/megatron/core/tensor_parallel/layers.py

class ColumnParallelLinear(torch.nn.Module):

“”” The linear layer is defined as Y = XA + b. A is parallelized along its second dimension as A = [A_1, …, A_p]. “””

def __init__(self, gather_output=False）：

#输出是否需要进行all-gather操作

self.gather_output = gather_output

def forward(self):

#1.对输入数据进行处理

#算子F操作：复制

input_parallel = copy_to_tensor_model_parallel_region(input_)

#2.矩阵乘法操作 Y=XA

output_parallel = linear_with_grad_accumulation_and_async_allreduce()

#3.对输出数据进行处理

#算子G操作：

if self.gather_output：

#执行all-gather

output = gather_from_tensor_model_parallel_region(output_parallel)

else:

#不执行all-gather

output = output_parallel

2.2.3 F算子和G算子

F算子和G算子的实现：

  • F算子：_CopyToModelParallelRegion

    • forward：identity 操作，把输入 X 完整的分发到每个GPU。
    • backward：all-reduce操作，对X的梯度进行求和操作，得到完整的梯度。
  • G算子：_GatherFromModelParallelRegion

    • forward：all-gather 操作，把输出的各个Yi进行合并，得到完整的Y。
    • backward：split操作，对Y的梯度进行切分，分发到每个GPU。

源码：/megatron/core/tensor_parallel/mappings.py

#1、算子F

def copy_to_tensor_model_parallel_region(input_):

return _CopyToModelParallelRegion.apply(input_)

class _CopyToModelParallelRegion(torch.autograd.Function):

@staticmethod

def forward(ctx, input_):

#算子F的复制操作

return input_

@staticmethod

def backward(ctx, grad_output):

#算子F对梯度进行all-reduce操作

return _reduce(grad_output)

#2、算子G

def gather_from_tensor_model_parallel_region(input_):

return _GatherFromModelParallelRegion.apply(input_)

class _GatherFromModelParallelRegion(torch.autograd.Function):

@staticmethod

def forward(ctx, input_):

#算子G的all-gather操作

return _gather_along_last_dim(input_)

@staticmethod

def backward(ctx, grad_output):

#算子G对梯度进行split

return _split_along_last_dim(grad_output)

2.3 RowParallelLinear

2.3.1 原理分析

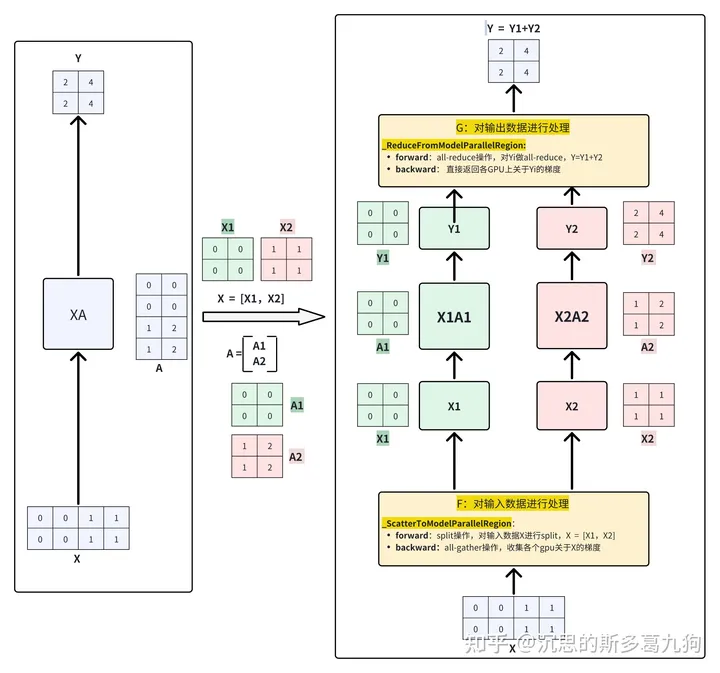
在Megatron-LM中，不能只考虑列并行矩阵乘法，还需要考虑模型的前向传播和后向传播过程，通过加入F和G算子，每个算子都包含forward和backward操作，分别对输入和输出数据进行处理，进而实现模型训练流程。

forward流程：

  • step1：通过F算子对输入数据进行处理。

    • F算子：split操作，对输入X进行切分，Xi分发到每个GPU。
  • step2：矩阵乘法。
  • step3：通过G算子对输出数据进行处理。

    • G算子：all-reduce操作，对输出Yi进行求和操作，得到完整的结果Y。

IMG_267

2.3.2 源码解读

RowParallelLinear的forward流程如下所示：

源码：/megatron/core/tensor_parallel/layers.py

class RowParallelLinear(torch.nn.Module):

“”” – – | A_1 | | . | A = | . | X = [X_1, …, X_p] | . | | A_p | – – “””

def __init__(self,input_is_parallel = False)

#判断输入是不是已经切分好的[X_1, …, X_p]

self.input_is_parallel = input_is_parallel

def forward(self, input_):

#1.对输入数据进行处理

if self.input_is_parallel:

#已经切分好的Xi，直接返回

input_parallel = input_

else:

#算子F操作：切分X，Xi分发到每个GPU

input_parallel = scatter_to_tensor_model_parallel_region(input_)

#2.矩阵乘法

output_parallel = linear_with_grad_accumulation_and_async_allreduce()

#3.对输出数据进行处理

#算子G操作：对Yi进行all-reduce求和

output_ = reduce_from_tensor_model_parallel_region(output_parallel)

2.3.3 F算子和G算子

F算子和G算子的实现：

  • F算子：_ScatterToModelParallelRegion

    • forward：split操作，对输入X进行切分，Xi分发到每个GPU。
    • backward：all-gather 操作，对各个GPU的Xi梯度进行合并，得到完整的X梯度。
  • G算子：_ReduceFromModelParallelRegion

    • forward：all-reduce操作，对输出Yi进行求和操作，得到完整的结果Y。
    • backward：identity操作，直接返回各个卡的梯度。

源码：/megatron/core/tensor_parallel/mappings.py

#F算子def scatter_to_tensor_model_parallel_region(input_):

return _ScatterToModelParallelRegion.apply(input_)

class _ScatterToModelParallelRegion(torch.autograd.Function):

@staticmethod

def forward(ctx, input_):

#split操作，对输入X进行切分，Xi分发到每个GPU。

return _split_along_last_dim(input_)

@staticmethod

def backward(ctx, grad_output):

#all-gather 操作，对各个GPU的Xi梯度进行合并，得到完整的X梯度。

return _gather_along_last_dim(grad_output)

#G算子def reduce_from_tensor_model_parallel_region(input_):

return _ReduceFromModelParallelRegion.apply(input_)

class _ReduceFromModelParallelRegion(torch.autograd.Function):

@staticmethod

def forward(ctx, input_):

#all-reduce操作，对输出Yi进行求和操作，得到完整的结果Y

return _reduce(input_)

@staticmethod

def backward(ctx, grad_output):

#identity操作，直接返回各个卡的梯度

return grad_output

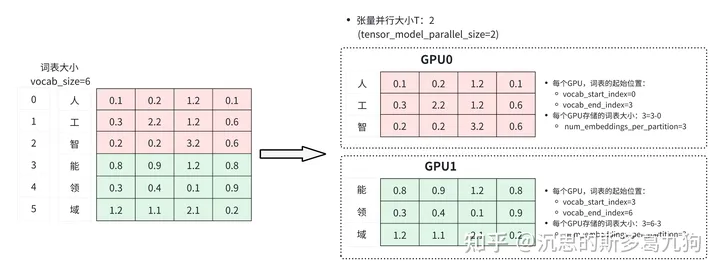
3.并行embed

3.1原理分析

VocabParallelEmbedding

简介：为了让内存做到均衡配置，Megatron-LM对embedding也会按照vocab维度来做切分操作，每个GPU上都有部分词表的embedding。

3.1.1 embed初始化

如下图所示：

IMG_268

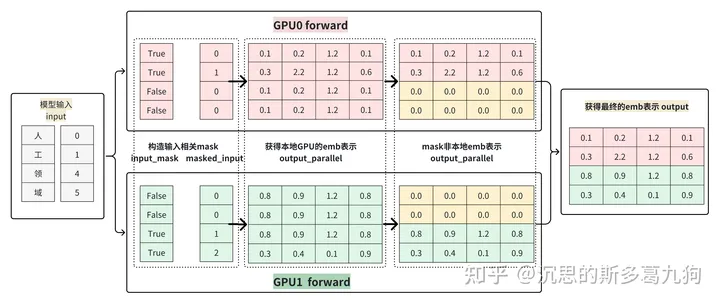
3.1.2 embed forward

forward流程如下图所示：

  • step1：根据输入input构造相关mask：input_mask和masked_input
  • step2：基于masked_input获得本地GPU的emb表示
  • step3：根据input_mask对非本地的存储的emb进行mask操作
  • step4：各GPU的emb进行all-reduce操作，得到最终的完整emb表达

IMG_269

3.2源码解读

class VocabParallelEmbedding(torch.nn.Module):

def __init__(self, num_embeddings: int, embedding_dim: int, ):

#每个GPU的词表起始位置

self.vocab_start_index, self.vocab_end_index =VocabUtility.vocab_range_from_global_vocab_size()

#每个GPU存储的词表大小

self.num_embeddings_per_partition = self.vocab_end_index – self.vocab_start_index

#根据词表大小和维度初始化该GPU的emb矩阵

self.weight = Parameter(torch.empty(

self.num_embeddings_per_partition, self.embedding_dim))

def forward(self, input_):

def forward(self, input_):

# step1:根据输入，构造mask

input_mask = (input_ < self.vocab_start_index) | \

(input_ >= self.vocab_end_index)

# Mask the input.

masked_input = input_.clone() – self.vocab_start_index

masked_input[input_mask] = 0

#step2:获得本地的emb表示

output_parallel = F.embedding(masked_input, self.weight,

self.padding_idx, self.max_norm,

self.norm_type, self.scale_grad_by_freq,

self.sparse)

# Mask the output embedding.

#step3: 对非本地的存储的emb进行mask操作

output_parallel[input_mask, :] = 0.0

# Reduce across all the model parallel GPUs.

#step4: reduce操作，获得完整emb

output = reduce_from_tensor_model_parallel_region(output_parallel)

return output

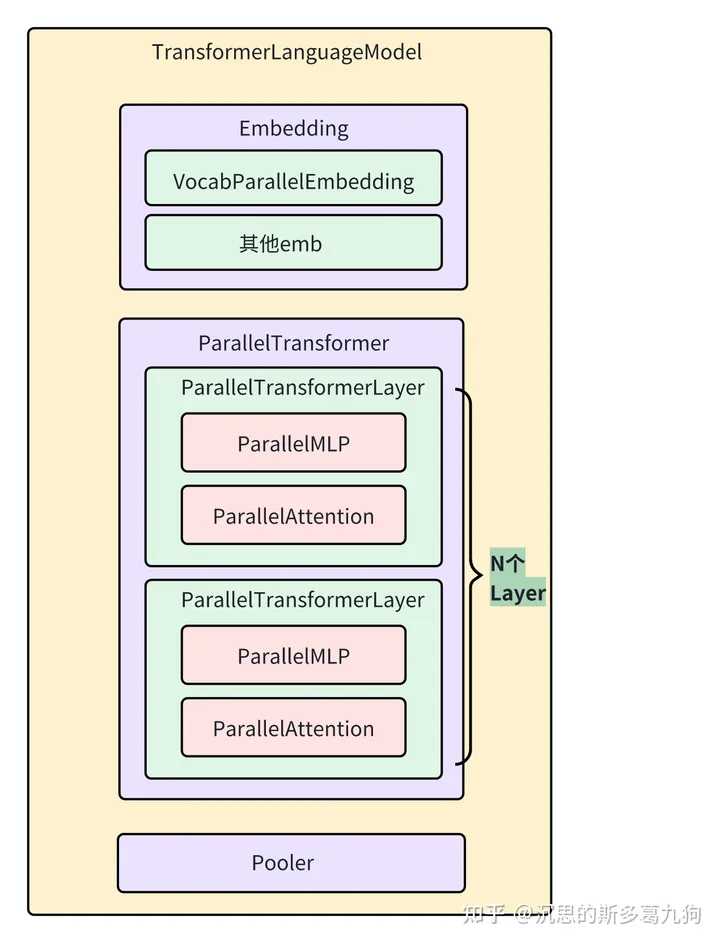
4.并行Transformer

4.1 transformer结构

如下图所示：

IMG_270

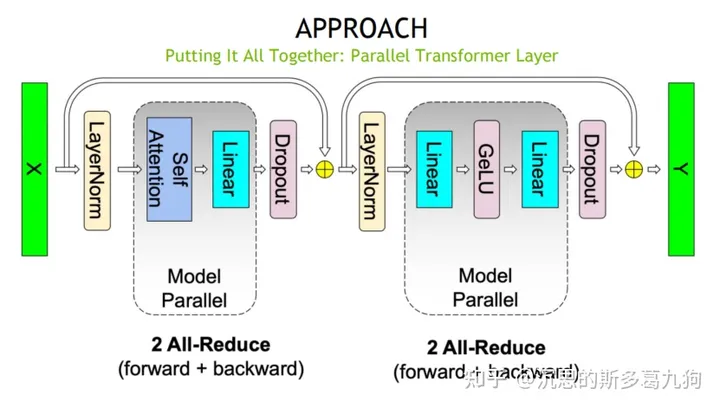
4.2通信量分析

一个ParallelTransformer层，有4次all-reduce操作，其中MLP和Attention各2次all-reduce。

IMG_271

参考

https://developer.nvidia.com/gt

© 版权声明
THE END
AI资讯
喜欢就支持一下吧
点赞5 分享
feidan的头像-
边界AIChat使用教程-
边界AIChat使用教程
边界AIChat使用教程
9个月前 8947
【全面对比】6款AI生成PPT工具评测：免费与实用兼具，哪款更胜一筹？-
【全面对比】6款AI生成PPT工具评测：免费与实用兼具，哪款更胜一筹？
【全面对比】6款AI生成PPT工具评测：免费与实用兼具，哪款更胜一筹？
4个月前 8248
清华系AI对比评测：智谱清言与Kimi Chat的功能与优势-
清华系AI对比评测：智谱清言与Kimi Chat的功能与优势
清华系AI对比评测：智谱清言与Kimi Chat的功能与优势
5个月前 7025
WPS最新破解版，已永久激活，无限制使用！-
WPS最新破解版，已永久激活，无限制使用！
WPS最新破解版，已永久激活，无限制使用！
9个月前 6638
国产神器，破姐资源一键下载，太强了-
国产神器，破姐资源一键下载，太强了
国产神器，破姐资源一键下载，太强了
9个月前 5827
权威发布：国产AI工具排行榜TOP10，必备神器一览无余-
权威发布：国产AI工具排行榜TOP10，必备神器一览无余
权威发布：国产AI工具排行榜TOP10，必备神器一览无余
5个月前 5651
相关推荐
【全面对比】6款AI生成PPT工具评测：免费与实用兼具，哪款更胜一筹？-
【全面对比】6款AI生成PPT工具评测：免费与实用兼具，哪款更胜一筹？
【全面对比】6款AI生成PPT工具评测：免费与实用兼具，哪款更胜一筹？
4个月前 8248
清华系AI对比评测：智谱清言与Kimi Chat的功能与优势-
清华系AI对比评测：智谱清言与Kimi Chat的功能与优势
清华系AI对比评测：智谱清言与Kimi Chat的功能与优势
5个月前 7025
权威发布：国产AI工具排行榜TOP10，必备神器一览无余-
权威发布：国产AI工具排行榜TOP10，必备神器一览无余
权威发布：国产AI工具排行榜TOP10，必备神器一览无余
5个月前 5651
字节跳动旗下Dreamina：一款免费且强大的国产AI绘画工具-
字节跳动旗下Dreamina：一款免费且强大的国产AI绘画工具
字节跳动旗下Dreamina：一款免费且强大的国产AI绘画工具
7个月前 1133
评论 抢沙发
头像
欢迎您留下宝贵的见解！
提交
头像

昵称

取消
昵称

请填写用户信息：

  • 昵称(必填)
  • 邮箱(必填)
表情
[aoman][baiyan][bishi][bizui][cahan][ciya][dabing][daku][deyi][doge][fadai][fanu][fendou][ganga][guzhang][haixiu][hanxiao][zuohengheng][zhuakuang][zhouma][zhemo][zhayanjian][zaijian][yun][youhengheng][yiwen][yinxian][xu][xieyanxiao][xiaoku][xiaojiujie][xia][wunai][wozuimei][weixiao][weiqu][tuosai][tu][touxiao][tiaopi][shui][se][saorao][qiudale][se][qinqin][qiaoda][piezui][penxue][nanguo][liulei][liuhan][lenghan][leiben][kun][kuaikule][ku][koubi][kelian][keai][jingya][jingxi][jingkong][jie][huaixiao][haqian][aini][OK][qiang][quantou][shengli][woshou][gouyin][baoquan][aixin][bangbangtang][xiaoyanger][xigua][hexie][pijiu][lanqiu][juhua][hecai][haobang][caidao][baojin][chi][dan][kulou][shuai][shouqiang][yangtuo][youling]
代码

请输入代码：

确认
图片

    暂无评论内容

搜索
开启精彩搜索
边界AIChat使用教程-
8947人已阅读
边界AIChat使用教程
TOP1
【全面对比】6款AI生成PPT工具评测：免费与实用兼具，哪款更胜一筹？-
【全面对比】6款AI生成PPT工具评测：免费与实用兼具，哪款更胜一筹？
4个月前8248人已阅读
TOP2
清华系AI对比评测：智谱清言与Kimi Chat的功能与优势-
清华系AI对比评测：智谱清言与Kimi Chat的功能与优势
5个月前7025人已阅读
TOP3
WPS最新破解版，已永久激活，无限制使用！-
WPS最新破解版，已永久激活，无限制使用！
9个月前6638人已阅读
TOP4
国产神器，破姐资源一键下载，太强了-
国产神器，破姐资源一键下载，太强了
9个月前5827人已阅读
TOP5
权威发布：国产AI工具排行榜TOP10，必备神器一览无余-
权威发布：国产AI工具排行榜TOP10，必备神器一览无余
5个月前5651人已阅读
TOP6