LLM训练06 流水线并行

分布式训练topic由以下几部分组成：

1、朴素的模型并行

1.1 简介

原理：假设有K个GPU，把一个L层的模型切分成K份，每个GPU拥有模型层数是L/K层。

简介：如下图所示，类似串行的思想。

数据先依次在GPU0 –> GPU1 –> GPU2 上进行forward前向计算，然后依次在GPU2 –> GPU1 –> GPU0 上进行backward反向计算。

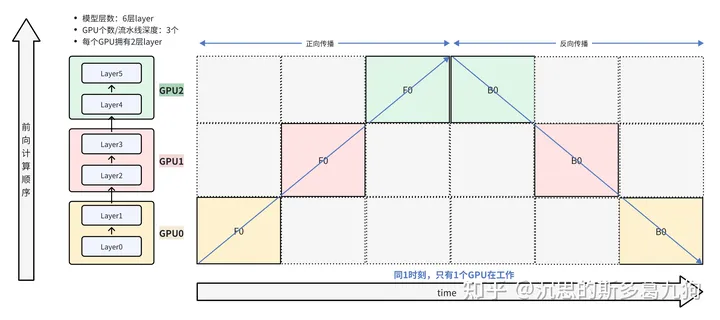
问题：

计算效率：GPU利用率低，同一时刻只有一个GPU被利用，其余GPU处于空闲状态(图中灰色的格子，又称气泡bubble)。
显存效率：显存占用高，每一个GPU需要保存完整的输入激活值显存占用。

1.2 代码实现

上图的代码实现

import torchimport torch.nn as nnimport torch.optim as optim

class NaiveParallelModel(nn.Module):

def __init__(self):

super(NaiveParallelModel, self).__init__()

hidden_size=10

# 一共有6个layer

self.net0 = nn.Linear(hidden_size,hidden_size)

self.net1 = nn.Linear(hidden_size, hidden_size)

self.net2 = nn.Linear(hidden_size, hidden_size)

self.net3 = nn.Linear(hidden_size, hidden_size)

self.net4 = nn.Linear(hidden_size, hidden_size)

self.net5 = nn.Linear(hidden_size, hidden_size)

self.relu = nn.ReLU()

#每个GPU拥有2个layer

self.seq0 = nn.Sequential(self.net0, self.relu, self.net1,self.relu ).to(“cuda:0”)

self.seq1 = nn.Sequential(self.net2, self.relu, self.net3, self.relu).to(“cuda:1”)

self.seq2 = nn.Sequential(self.net4, self.relu, self.net5).to(“cuda:2”)

def forward(self,x):

#串行的方式，同一时刻只有一个GPU被利用

x = self.seq2(self.seq1(self.seq0(x).to(“cuda:1”)).to(“cuda:2”))

return x

def train_naive_PP():

batch_size = 16

hidden_size = 10

model = NaiveParallelModel()

inputs = torch.randn(batch_size,hidden_size).to(“cuda:0”)

labels = torch.randn(batch_size,hidden_size).to(“cuda:2”)

loss_fn = nn.MSELoss()

optimizer = optim.SGD(model.parameters(), lr=1e-3)

optimizer.zero_grad()

outputs = model(inputs)

loss= loss_fn(outputs,labels)

loss.backward()

optimizer.step()

if __name__ == ‘__main__’:

train_naive_PP()

train_pp()

2、GPipe

论文：

GPipe: Efficient Training of Giant Neural Networks using Pipeline Parallelism 2018 google

torchgpipe: On-the-fly Pipeline Parallelism for Training Giant Models 2020

目标：解决朴素模型并行的资源浪费问题，减少空闲气泡大小bubble。

解决办法：引入数据并行思想，对数据进行切分，把1个小批量(mini-batch)切成M个微批量（micro-batch），每一次在1个微批量micro-batch上进行计算。（梯度累积的思想）

Lingvo框架：基于TensorFlow的实现。
torchpipe：基于Torch的复现。

2.1 简介

如下图所示。

(1)数据拆分：将1个batch的数据，拆分为4个微批次： FX0/FX1/FX2/FX3

(2)前向计算：对4个微批次数据依次进行前向计算。

第0个微批次数据 FX0 先依次在GPU0 –> GPU1 –> GPU2 上进行forward前向计算
- F00 / GPU0 –> F10 / GPU1 –> F20 / GPU2
第1个微批次数据 FX1 重复上述前向计算
第2个微批次数据 FX2 重复上述前向计算
第3个微批次数据 FX3 重复上述前向计算

(3)反向计算：待4个微批次数据全部完成前向计算（梯度一直在微批次中累积），才开始反向计算。

第3个微批次数据 FX3 先依次在GPU2 –> GPU1 –> GPU0 上进行backward反向计算
- F23 / GPU2 –> F13 / GPU1 –> F03 / GPU2
第2个微批次数据 FX2 重复上述反向计算
第1个微批次数据 FX1 重复上述反向计算
第0个微批次数据 FX0 重复上述反向计算

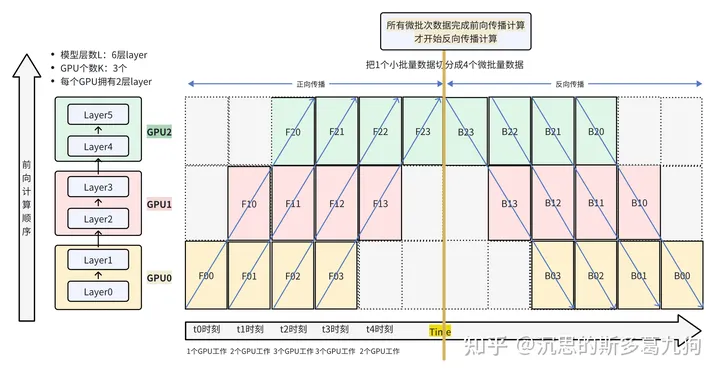
2.2 空闲气泡bubble计算

符号说明：与paper保持一致。

L：模型的层数，eg：L=6
K：GPU个数/流水线深度p，eg：K=3
L/K：每个GPU的层数, eg: L/K=2
N：mini batch size，模型输入数据个数(bs)，小批量的数据个数 , eg：N=16
M：切的块数，微批次的数量， eg： M=4
N/M：micro batch size，微批量下模式下的模型输入数据个数, eg: N/M=4

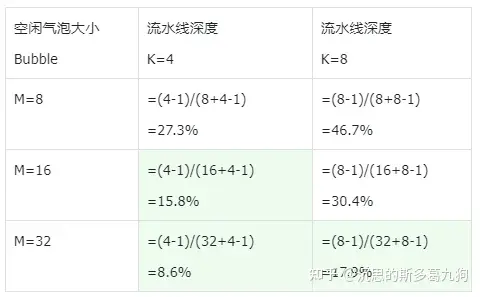
计算逻辑如下:

长度：2*（M+K-1）
宽度：K
总体面积：K*2*(M+K-1)
利用的GPU面积：(2*M*K)
利用的GPU占比： (2*M*K)/(K*2*(M+K-1))
空闲的GPU占比（bubble）：1- 2*M*K/K*2*（M+K-1） = 1-M/（M+K-1) = (K-1)/(M+K-1)

结论：

M(micro-batch)越大，同一时刻满负荷运行的GPU个数越多，空闲的气泡bubble越少。
当 M≥ 4*K 时，气泡大小可忽略不计。

2.3 中间激活值显存占用

2.3.1 没有重计算

简介：每个块都保留完整的输入数据。

L：模型的层数，eg：L=6
K：GPU个数/流水线深度，eg：K=3
L/K：每个GPU的层数, eg: L/K=2
N：mini batch size，模型输入数据个数(bs)，小批量的数据个数 , eg：N=16
M：切的块数，微批量块，指令长度， eg： M=4
N/M：micro batch size，微批量下模式下的模型输入数据个数, eg: N/M=4

每个GPU中间激活值显存：每个GPU的层数 * 数据个数 = （）O（LK∗N） eg： O(2*N)

2.3.2 引入重计算

核心思路：删掉中间变量的激活值占用

简介：每个块只保留一份中间值(边界层的中间值)。同时，保留一份完整的输入数据（在反向传播时，用于重计算所需的中间变量）。

微批量的中间值： O(LK∗NM) eg： 0.5*N
模型输入数据个数：N

每个GPU中间激活值显存： O(N+LK∗NM) ， eg：O(1.5*N)

2.4 怎么切

Gpipe就是依据算力对图进行了分割，从而把不同层分配到不同的GPU。

Megatron-LM的切法：直接按照层数切分。

ParallelTransformer一共有6个ParallelTransformerLayer，
流水行深度/GPU个数=3
每个GPU拥有的ParallelTransformerLayer个数：num_layers=6//3=2

#megatron/model/transformer.pydef _get_num_layers(args, model_type, is_decoder=False):

…

num_layers = args.num_layers // args.transformer_pipeline_model_parallel_size

…

return num_layers

2.5 代码实现

上图中的代码实现：

class ParallelModel(nn.Module):

def __init__(self,split_size):

super(ParallelModel, self).__init__()

hidden_size=10

# 一共有6个layer

self.net0 = nn.Linear(hidden_size,hidden_size)

self.net1 = nn.Linear(hidden_size, hidden_size)

self.net2 = nn.Linear(hidden_size, hidden_size)

self.net3 = nn.Linear(hidden_size, hidden_size)

self.net4 = nn.Linear(hidden_size, hidden_size)

self.net5 = nn.Linear(hidden_size, hidden_size)

self.relu = nn.ReLU()

# 每个GPU拥有2个layer

self.seq0 = nn.Sequential(self.net0, self.relu, self.net1,self.relu ).to(“cuda:0”)

self.seq1 = nn.Sequential(self.net2, self.relu, self.net3, self.relu).to(“cuda:1”)

self.seq2 = nn.Sequential(self.net4, self.relu, self.net5).to(“cuda:2”)

self.split_size=split_size

def forward(self,x):

#将将1个batch的数据，拆分为split_size个微批次数据

splits = iter(x.split(self.split_size, dim=0))

s_next = next(splits)

# 第一个微批次起点

s_prev = self.seq0(s_next).to(“cuda:1”)

ret =[]

for s_next in splits:

s_prev = self.seq1(s_prev).to(“cuda:2”)

s_prev = self.seq2(s_prev)

ret.append(s_prev)

#下一个微批次起点

s_prev=self.seq0(s_next).to(“cuda:1”)

#最后一个微批次

s_prev = self.seq1(s_prev).to(“cuda:2”)

s_prev = self.seq2(s_prev)

ret.append(s_prev)

return torch.cat(ret)

def train_naive_PP():

batch_size = 16

hidden_size = 10

model = NaiveParallelModel()

inputs = torch.randn(batch_size,hidden_size).to(“cuda:0”)

labels = torch.randn(batch_size,hidden_size).to(“cuda:2”)

loss_fn = nn.MSELoss()

optimizer = optim.SGD(model.parameters(), lr=1e-3)

optimizer.zero_grad()

outputs = model(inputs)

loss= loss_fn(outputs,labels)

loss.backward()

optimizer.step()

if __name__ == ‘__main__’:

train_pp()

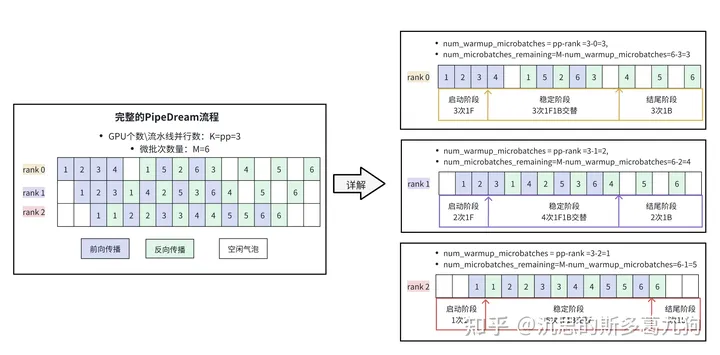
3、PipeDream

论文：PipeDream ：Memory-Efficient Pipeline-Parallel DNN Training 2020 微软

问题：Gpipe流水线其存在两个问题：GPU利用率低（bubble气泡），显存占用大。

Gpipe显存占用分析：所有微批次完成前向传播计算，才开始反向传播计算。每个GPU需要缓存M份中间激活值。

目标：需要每个微批次数据尽可能早的完成反向传播计算，从而使得对应的中间激活值可以提前释放。

解决方案： 1F1B策略。

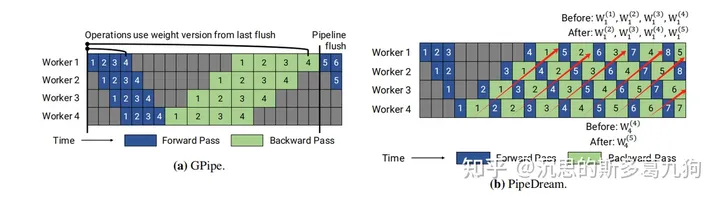
3.1 1F1B策略

简介：One Forward pass followed by One Backward pass。1个微批次完成前向传播计算，就开始反向传播计算。

如上图b红色箭头所示，1个微批次数据在完成前向传播以后，立刻开始反向传播。这样子微批次数据对应的中间激活值就可以提前释放。

3.1.1 训练有效性问题

在这种1F1B训练模式下，前向传播和反向传播是相互交错的。每1个微批次数据反向传播后，模型参数会更新，若干个微批次数据进行反向传播后，会带来多个版本权重参数，也就容易出现同一个批次数据采用不同版本的模型权重参数。

问题1：同一个微批次数据，相同的device（相同stage），在前向计算和反向计算，采用不同版本的模型参数。

示例：

Device 1 的微批次5数据，在前向传播使用了第1个版本模型（微批次1反向传播完成），
Device 1 的微批次5数据，在反向传播使用了第4个版本模型（微批次1、2、3、4反向传播完成）

解决办法：Weight Stashing方法

每个device多备份几个不同版本的权重，确保同一个微批次数据，在前向计算和后向计算采用同一个版本的模型权重。计算前向传播之后，会将这份前向传播使用的权重保存下来，用于同一个 minibatch 的后向计算。

示例：

Device 1 的微批次5数据，在前向传播使用了第1个版本模型（微批次1反向传播完成），
Device 1 的微批次5数据，在反向传播使用了第1个版本模型（微批次1反向传播完成）

问题2：同一个微批次数据，相同的操作（都是前向或者都是反向），在不同的device上（不同stage），采用不同版本的模型参数。

示例：

Device 1 的微批次5数据，在前向传播使用了第1个版本模型（微批次1反向传播完成）
Device 2 的微批次5数据，在前向传播使用了第2个版本模型（微批次1、2反向传播完成）

解决方法：Vertical Sync 方法。

每个批次数据进入pipeline时都使用当前device（阶段）最新版本的参数，并且参数版本号会伴随该批次数据整个生命周期，从而实现了device（阶段）间的参数一致性。

示例：

Device 1 的微批次5数据，在前向传播使用了第1个版本模型（微批次1反向传播完成）
Device 2 的微批次5数据，在前向传播使用了第1个版本模型（微批次1反向传播完成）

3.1.2 非交错式 schedule

源码：megatron/core/pipeline_parallel/schedules.py

调度模式：

1F1B有两种调度模式：

（1）非交错式 schedule：默认的模式，如下图中的top figure。

Megatron-LM：forward_backward_pipelining_without_interleaving方法

（2）交错式 schedule：如下图中的bottom figure。

Megatron-LM：forward_backward_pipelining_with_interleaving方法

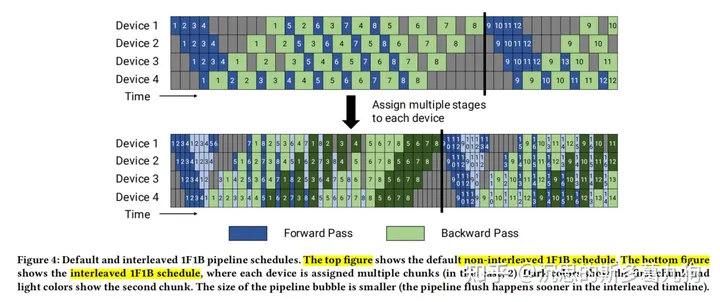
非交错式 schedule 可分为三个阶段：

第一阶段：启动热身阶段。微批次的前向传播，直到完成第1个小批次的前向传播。

第二阶段：稳定阶段。交替执行后续微批次的前向传播和反向传播。

第三阶段：结尾阶段。微批次的反向传播，对应着启动热身阶段的前向传播。

如下图所示：

参考

https://icml.cc/media/icml-2021/Slides/10457.pdf

https://pytorch.org/tutorials/i

THE END

AI资讯