前世今生
深度学习作为一种突破性技术，取得了显著的成功（1, 2），它主要运行在传统的冯·诺依曼计算硬件上。这项技术目前面临高能耗问题，例如GPT-3的1.3吉瓦时（GWh）的电力使用（3），以及计算速度慢（4）。由于这些挑战，研究人员正在探索用于人工神经网络（ANNs）的替代物理平台，包括光学（5-9）、自旋电子学（10,11）、纳米电子设备（12-15）、光子硬件（5）和声学系统（16,17）。
目前，神经网络硬件设计主要有两种方法。第一种是通过严格的操作对操作的数学同构来设计硬件，实现训练好的数学变换，主要针对深度学习的推理阶段（18-21）。第二类，深度物理神经网络（PNNs），专注于直接训练硬件的物理变换以执行所需的计算。PNNs通过利用物理变换并消除传统的软件-硬件分离，有望实现更可扩展、能效更高、速度更快的神经网络硬件（22, 23）。
到目前为止，PNNs的训练主要依赖于反向传播（BP）（24）。然而，BP并不适用于PNNs，原因之一是BP操作在硬件中的物理实现复杂且缺乏可扩展性（25-28）。通常，PNN提议使用in silico训练，在外部计算机上使用物理系统的数字孪生进行BP计算。然而，这种方法可能会因为物理系统的不准确表示而导致潜在的模拟-现实差距（6-8, 10, 13, 14, 20, 29, 30）。此外，基于BP的物理感知训练方法（PA-BP）（22）提供了对传统in silico方法的改进，但仍然需要一个可微分的数字模型来进行反向传递。此外，PA-BP训练的PNNs在受到强烈扰动时可能面临挑战，可能导致精细调整的模型无法使用，需要从头开始重新训练。
BP的另一个重要缺点是它依赖于完全了解前向传递期间执行的计算图，以准确计算导数（23, 31-34）。当在前向传递中插入一个黑盒时，BP变得不可行。因此，PNNs的替代训练方法已被证明是有利的。例如，探索用于训练物理网络的方法之一是增强的直接反馈对齐（DFA）方法（23），该方法旨在避免需要一个可微分的数字模型。然而，这种方法只与某些物理网络兼容，其中可以分离非线性和线性层。
局部学习已经被广泛研究用于训练数字神经网络，从Hopfield模型中的Hebbian对比学习早期工作（35）到最近的生物学合理框架（31, 34, 36, 37），分块BP（38, 39）和对比表示学习（40, 41）。受这一概念的启发，并为了解决基于BP的PNN训练的限制，作者提出了一种简单且与物理兼容的PNN架构，通过物理局部学习（PhyLL）算法增强。
提出的方法能够在不需要了解非线性物理层和训练数字孪生模型的情况下，对任意PNN进行监督和非监督对比学习训练。在这种无BP的方法中，通常由数字计算机执行的标准反向传递被物理系统的额外单一前向传递所取代。这种替代可以提高基于波的PNNs在训练阶段的训练速度、功耗和内存使用，通过消除其他硬件感知框架中存在的数字孪生建模阶段带来的额外开销。
作者展示了所提出方法的鲁棒性和适应性，即使在暴露于不可预测的外部扰动的系统中也是如此。为了展示方法的普适性，作者使用三种基于波的系统进行了实验性的元音和图像分类，这些系统在底层波现象和涉及的非线性类型方面有所不同。
匠心独运
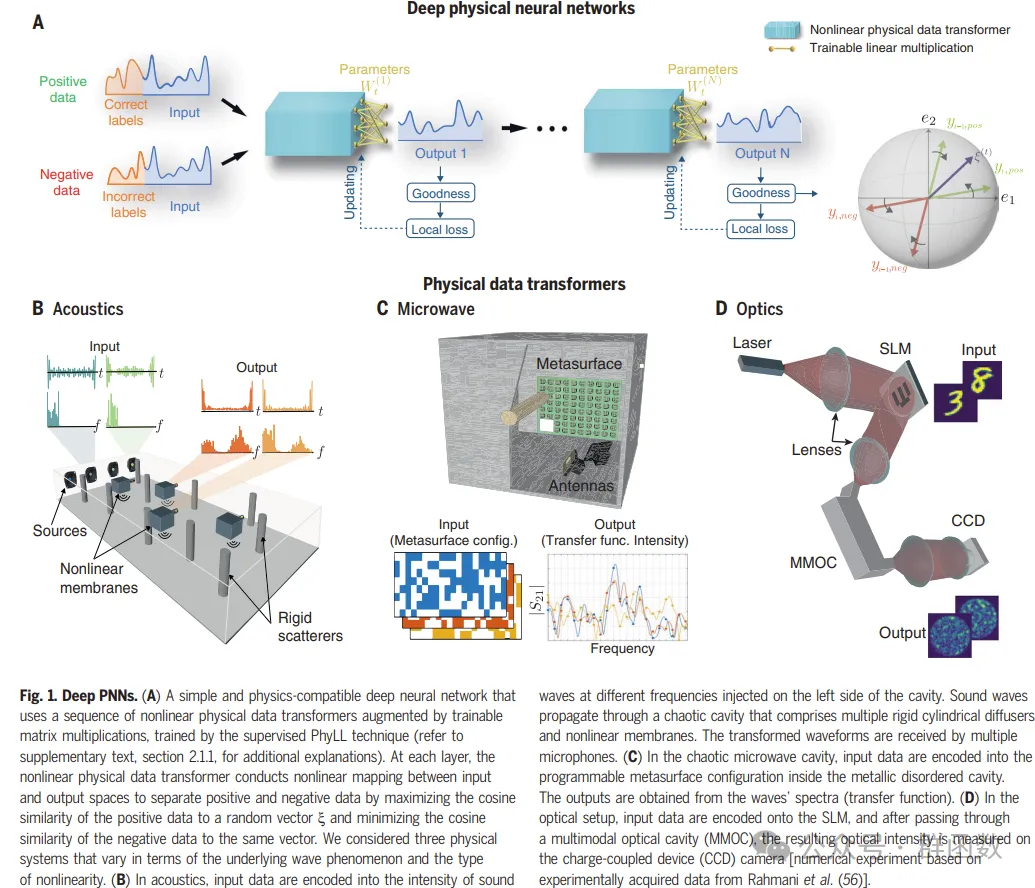图1. 深度PNNs。(A) 一个简单且与物理兼容的深度神经网络，它使用一系列非线性物理数据变换器，并通过可训练的矩阵乘法增强，通过监督的PhyLL技术进行训练（详见补充文本，第2.1.1节，以获得更多解释）。在每一层，非线性物理数据变换器在输入和输出空间之间进行非线性映射，通过最大化正数据与随机向量x的余弦相似度，以及最小化负数据与同一向量的余弦相似度，来分离正负数据。考虑了三种物理系统，它们在底层波现象和非线性类型方面有所不同。(B) 在声学中，输入数据被编码为在腔体左侧注入的不同频率的声波的强度。声波通过包含多个刚性圆柱形扩散器和非线性膜的混沌腔体传播。变换后的波形由多个麦克风接收。(C) 在混沌微波腔中，输入数据被编码为金属混乱腔体内的可编程超表面配置。输出是从波的频谱（传递函数）中获得的。(D) 在光学设置中，输入数据被编码到空间光调制器（SLM）上，通过多模光学腔（MMOC）后，产生的光强度在电荷耦合器件（CCD）相机上测量。
卓越性能
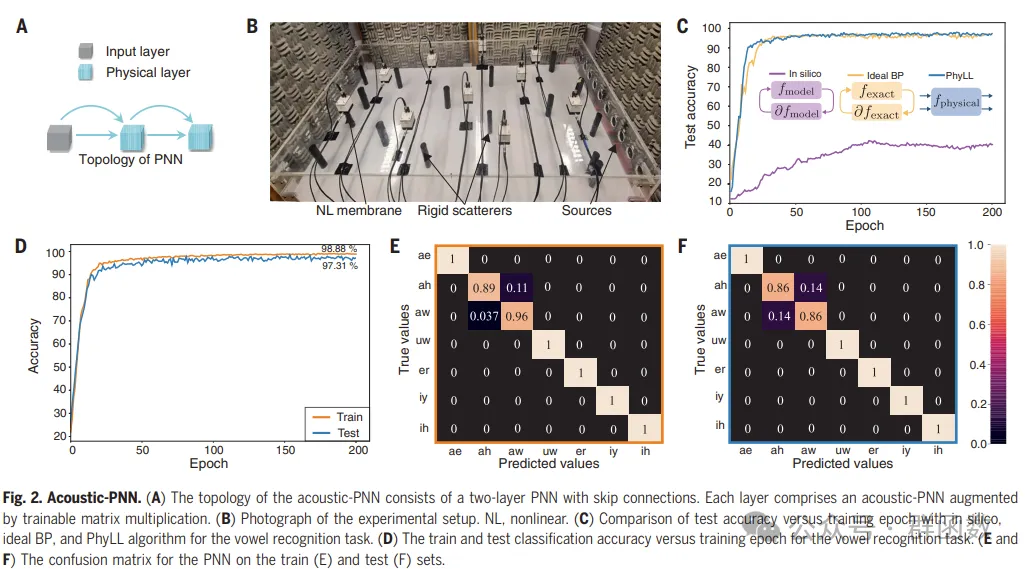
图2. 声学-PNN。(A) 声学-PNN的拓扑结构由一个带跳过连接的两层PNN组成。每层包括一个通过可训练矩阵乘法增强的声学-PNN。(B) 实验设置的照片。NL，非线性。(C) 对比测试精度与训练周期，使用in silico（计算机模拟）、理想的BP（反向传播）和PhyLL算法进行元音识别任务。(D) 训练和测试分类精度与训练周期的关系，用于元音识别任务。(E和F) PNN在训练(E)和测试(F)集上的混淆矩阵。
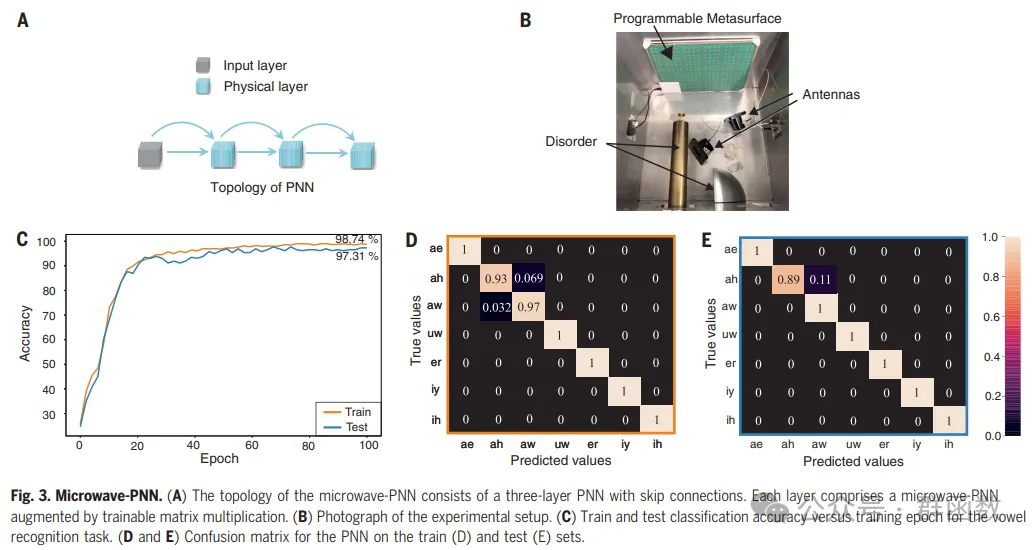
图3. 微波-PNN。(A) 微波-PNN的拓扑结构由一个带跳过连接的三层PNN组成。每层包括一个通过可训练矩阵乘法增强的微波-PNN。(B) 实验设置的照片。(C) 元音识别任务的训练和测试分类精度与训练周期的关系。(D和E) PNN在训练(D)和测试(E)集上的混淆矩阵。
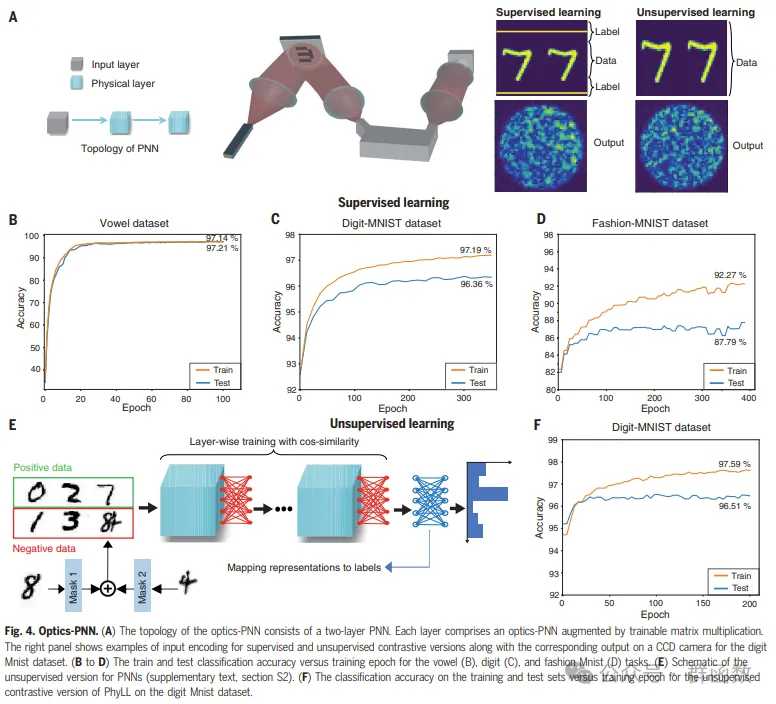
图4. 光学-PNN。(A) 光学-PNN的拓扑结构由一个两层PNN组成。每层包括一个通过可训练矩阵乘法增强的光学-PNN。右侧面板显示了监督和非监督对比版本输入编码的示例，以及对应的在CCD相机上的输出，用于数字Mnist数据集。(B至D) 训练和测试分类精度与训练周期的关系，分别用于元音(B)、数字(C)和时尚Mnist(D)任务。(E) PNNs的非监督版本的示意图（补充文本，第S2节）。(F) 在数字Mnist数据集上，非监督对比版本的PhyLL在训练和测试集上的分类精度与训练周期的关系。
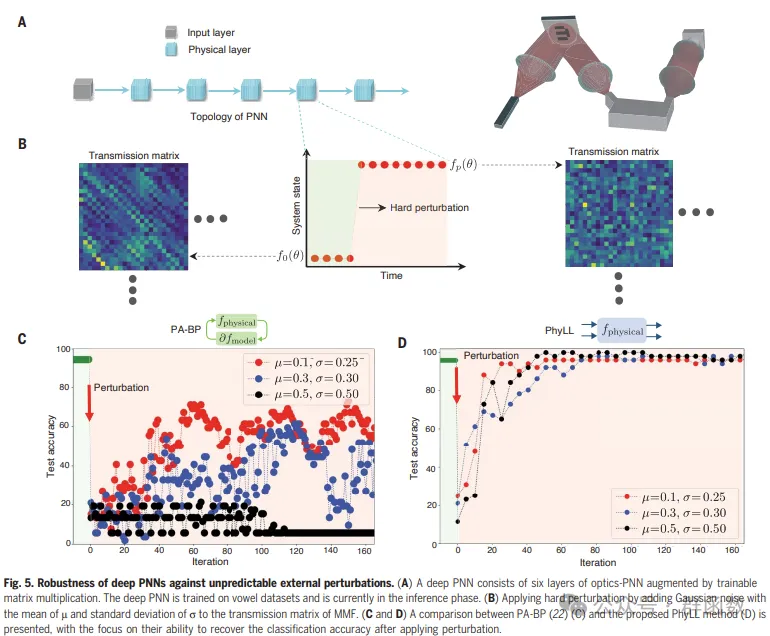
图5. 深度PNN对抗不可预测外部扰动的鲁棒性。(A) 一个深度PNN由六层光学-PNN组成，并通过可训练的矩阵乘法增强。深度PNN在元音数据集上进行了训练，目前处于推理阶段。(B) 通过向多模光纤（MMF）的传输矩阵添加均值为m、标准差为s的高斯噪声，应用硬扰动。(C和D) 展示了PA-BP（22）(C)和提出的PhyLL方法(D)之间的比较，重点是它们在应用扰动后恢复分类精度的能力。
总结展望
由于人工神经网络（ANNs）的规模，如大型语言模型（LLMs）的空前增长，预计这种增长将持续不断，这些网络的训练和推理阶段的成本已经呈指数级增长。像PNNs这样的专用硬件有潜力大幅度降低这些成本。Anderson等人（21）最近预测，与数字电子处理器相比，对于大规模的未来变换器模型，推理时间能效优势约为8000倍。本文提出的训练方法可以作为训练这些光学LLMs的可行候选方案，可能提供显著的能效和速度优势。用光学实现大规模LLMs仍然面临一些挑战，例如当前的空间光调制器（SLM）容量限制在几百万参数——远远达不到所需的数十亿参数。然而，实现数十亿参数的光学架构和能效高的PNNs并没有根本性的障碍。
暂无评论内容