如果你熟悉当前LLM的主流架构，混合专家（MoE）技术想必是老朋友之一。有人甚至会说，MoE是使大模型崛起的关键因素之一。开源的Mixtral、DBRX、Grok等模型都使用了MoE，而且根据Soumith Chintala等大佬的推测，GPT-4也是一个规模为8×220B的MoE模型。
类似GPT-4，多数MoE模型都会将专家数量限制在较少数量，一般不会超过16或32。然而，DeepMind研究科学家Xu Owen He最近就在一篇独立发表的论文中，提出了一种全新的方法——PEER（参数高效专家检索，Parameter Efficient Expert Retrieval），可以将专家数量扩展到百万数量级。
论文地址：https://arxiv.org/abs/2407.04153这究竟是如何做到的？参数量不会爆炸吗？不会造成收益递减吗？如何实现能在百万个专家中实现高效检索？
背景与介绍
Transformer架构中，每个块内都包含注意力层和前馈层（FFW），注意力层用于计算序列中token之间的关系，FFW网络则负责存储模型知识。我们当然希望LLM能在参数中隐式存储更多知识，但FFW的计算成本和激活内存会随之线性增加。稠密模型中，FFW层已经占据了总参数量的2/3，是扩展的主要瓶颈之一。MoE模型虽然参数量也很大，但每次推理时不会动用整个模型的能力，而是将数据路由到小型且专门的「专家模块」，因此能在LLM参数增加的同时，让推理所需的计算成本基本不变。那么专家数量（即MoE模型的「粒度」）是不是越多越好？这要考虑多个因素，包括模型参数总量、训练token数量和算力的预算。2022年的一项研究认为，模型总参数量不变时，存在一个能达到最优性能的「最佳粒度」。专家数量超过这个与之后，模型性能就会进入「平台期」。
Unified Scaling Laws for Routed Language Models
论文地址：https://arxiv.org/pdf/2202.01169然而，今年年初Krajewski等人发表的一篇论文反驳了这个观点。他们发现，如果同时增加训练所用的token数量，那么更高粒度可以提高性能。
论文地址：https://arxiv.org/pdf/2402.07871受到这种细粒度MoE Scaling Law的启发，作者推断，模型容量的持续改进将带来具有高粒度的LLM，即包括大量微型专家的模型。除了能带来更高效的扩展，增加专家数量还有另外一层好处——终身学习。之前有研究表明，通过简单地添加新专家并进行适当正则化，MoE模型就可以适应连续的数据流。冻结旧专家、仅让新专家权重更新，就可以在保持可塑性的同时防止灾难性遗忘。在终身学习环境中，数据流可能达到无限长度，甚至永无止境，因此论文探索的专家数量的扩大就显得十分重要。
百万MoE所系
PEER层设计
形式上，PEER可以表达为函数
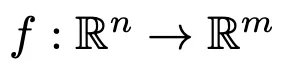
，包含如下三部分：– N个专家组成的专家池，其中每个专家ei和f有相同的函数签名
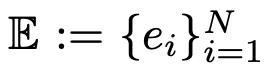– 一组相应的N个乘积键
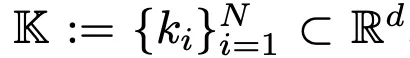– 用于将输入向量x映射到查询向量q(x)的查询网络
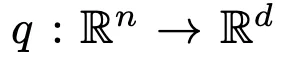
用𝒯𝑘表示top-k运算符，给定输入x，从N个专家中检索到k个专家的过程可以表示为：
之后使用softmax或sigmoid等激活函数应用于top-k个专家的查询-键内积，获得路由分数：
最后，计算路由分数加权的专家分数之和，作为PEER层输出。
上述的PEER层可以插入到Transformer架构骨干的中间，或者代替FFW层，整体计算流程如图2所示。
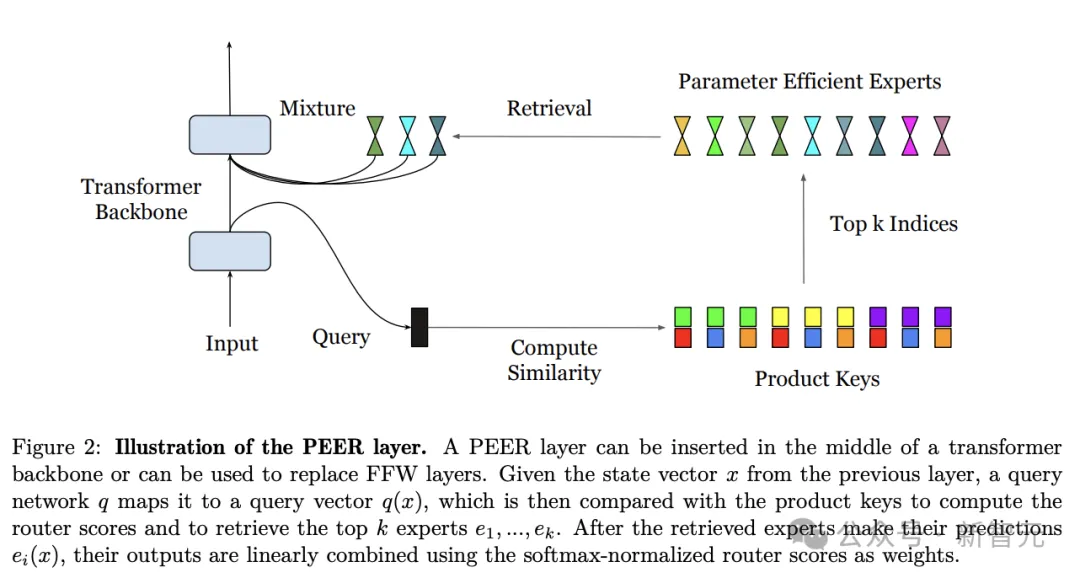
PEER层示意图
乘积键检索
由于要使用非常多的专家（N≥106），直接计算公式1中的前k个指标可能会非常耗费资源。为此，研究人员提出了乘积键检索技术——通过连接来自两个独立d/2维的子键C和C′（C, C′ ⊂ Rd/2）的向量来进行创建：
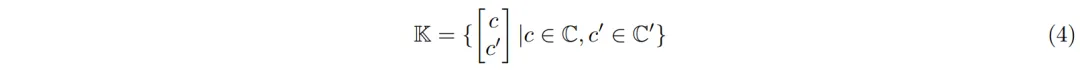
这种K的笛卡尔积结构，能够高效地找到前k位专家。也就是，先将查询向量q(x)拆分为两个子查询q1和q2，并分别对子查询与子键之间的内积进行前k个操作：
然后得到一组k2候选键集合，
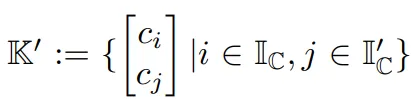
，在数学上，这可以保证从K中与q(x)最相似的k个键在这个候选集合中。此外，候选键与q(x)之间的内积只是子键与子查询之间内积的总和：
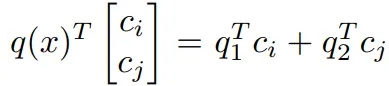
。因此，可以再次将前k个操作应用于这k的平方个内积，以从原始的乘积键集合K中获得前k个匹配键。最终，公式1中通过穷举搜索进行的top-k专家检索的复杂度，从O(N·d)降到了O((√N + k2)d)。
参数高效专家和多头检索
通常的MoE架构中会将专家隐藏层设计为FFW层相同大小，但PEER中的每个专家ei则小得多，仅仅是包含一个神经元、一个隐藏层的单例MLP：
其中vi、ui都不是参数矩阵，而是与x维度相同的向量，𝜎表示ReLU或GELU等激活函数。每个专家只有如此少的参数，怎么可能有强大的表达能力？此处，作者借鉴了多头注意力的做法，使用了「多头检索」（multi-head retrieval）机制。也就是说，查询过程并不是仅有一次，而是使用h个独立的查询网络，分别计算自己的查询向量并检索出一组top-k专家，但他们共享相同的专家池和每个专家的乘积键。h个「检索头」的输出相加后得到最终检索结果：
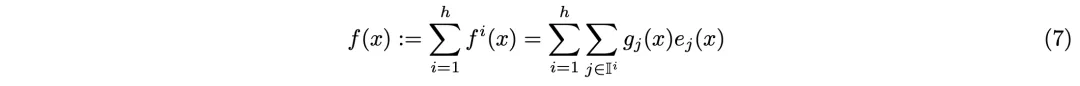
可以证明，当每个头只检索一名专家时（k=1），使用含h个检索头的PEER层，等效于使用含有h个神经元的专家。
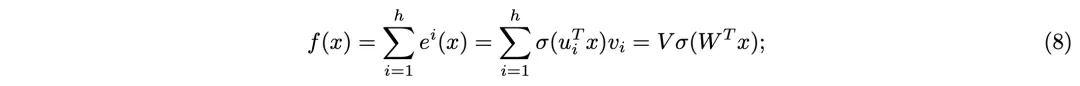
这就意味着，这种多头检索的过程相当于动态组装出含有h个神经元的专家MLP网络。与现有MoE中多个专家之间完全隔离的状态相比，这种设计允许专家间共享隐藏神经元，从而提升了参数效率和知识迁移的能力。算法1描述了PEER前向计算的简化实现。要想达到高效的实现，可能还需要专门的硬件内核来加速embedding查找，以及与einsum操作的融合。
为什么用大量的小专家
论文的背景介绍中，我们从直觉和经验层面推导出使用大量专家的优点，但作者也在此处用公式推导的方法证明了这一点。首先，我们可以用3个超参数表征MoE层的设置：参数总量P、每个token激活的参数Pactive以及单个专家的大小Pexpert。之前提及的，Krajewski论文中提出的「细粒度MoE Scaling Law」就可以用这三个参数表示为如下形式：
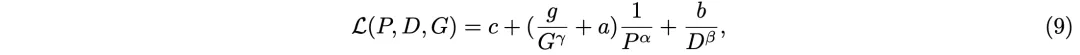
其中，L表示损失值，D是训练token总量，G是激活专家的数量，a、b、g、α、β、γ等字母都表示常量。为了降低损失值、提高模型性能，我们需要提升P、D、G的值，同时也需要限制Pactive的大小，因为计算和内存成本主要由激活参数量决定。值得注意的是，Pactive对应的内存占用也和batch中的token数量有关，但与batch大小或序列长度无关，因为在处理batch或序列的每个token时只需要存储模型的一份副本。由于专家大小Pexpert=Pactive/G，因此专家数量N=P/Pexpert=P·G/Pactive。这就意味着，如果想要在增加P、G的同时保持Pactive不变，就应该减小专家大小Pexpert，并增加专家数量N。这就解释了，我们为什么需要大量的小专家。一般来说，对于只有单个隐藏层的专家模型，其参数大小为：Pexpert=(2dmodel+1)dexpert，相应地，Pactive=(2dmodel+1)dactive。其中dmodel、dexpert、dactive分别表示表示Transformer的隐藏维度、单个专家的隐藏神经元数量以及每个token激活的参数总量。PEER中使用了尽可能小的专家大小，即dexpert=1，因此最大程度地降低了dactive，大小仅为检索头数量乘以每次检索的专家数量（h·k）。
实验
预训练isoFLOP分析
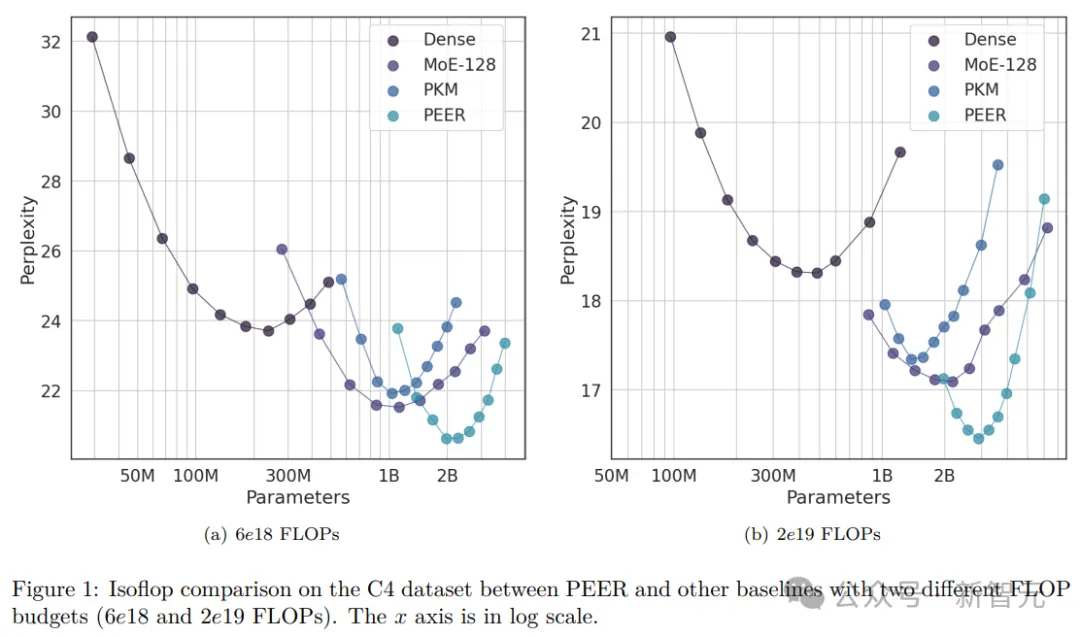
作者使用isoFLOP分析将PEER与各种基线方法进行了比较。这里，他选择了固定的FLOP预算（6e18和2e19），并同时改变模型大小和来自C4数据集的训练token数，以获得isoFLOP曲线。isoFLOP曲线上的每个点，都具有相同的计算成本，作者根据其模型大小和在C4上的最终验证困惑度（perplexity），来绘制这些点。对于密集基线模型，通过改变层数、注意力头数和模型维度来改变它们的大小。对于MoE、PKM和PEER方法，作者选取了每个考虑的密集模型，并分别用MoE、PKM和PEER层，替换中间块中的FFN层（例如，在12块Transformer中，替换第6块中的FFN）。在MoE中，作者使用了专家选择路由算法。该算法有效地解决了专家负载不平衡问题，并且通常优于token选择MoE。每个专家的大小与相应密集模型中原始MLP的大小相同，作者使用了128个专家来覆盖与PEER模型相同的模型大小范围。这种类型的MoE代表了标准的粗粒度方法，由少量大型专家组成。在PKM中，作者使用了1024×2个储存器，8个头，每个头选择32个存储器（top k=32）。此外，研究者还应用了查询批量归一化，这是原始PKM论文中推荐的，用于提高记忆使用率。在PEER中，同样使用了10242个专家，8个头，每个头选择16个存储器（top k=16）。默认情况下，作者也启用了查询批归一化（BatchNorm）来增加专家使用率。与专家选择MoE基线不同，PEER代表了一种细粒度方法，使用了大量小型专家。在所有模型大小和方法中，保持了一致的批大小（128）和序列长度（2048）。通过将总计算预算除以每个训练步骤的FLOP来计算训练步骤数。图1展示的是isoFLOP曲线。与密集FFW基线相比，稀疏替代方案使isoFLOP曲线向下和向右移动，因为其引入了更多的总参数P，但使用了更少或相同数量的活跃参数Pactive。另外，在相同的计算预算下，PEER模型达到了最低的计算优化困惑度。
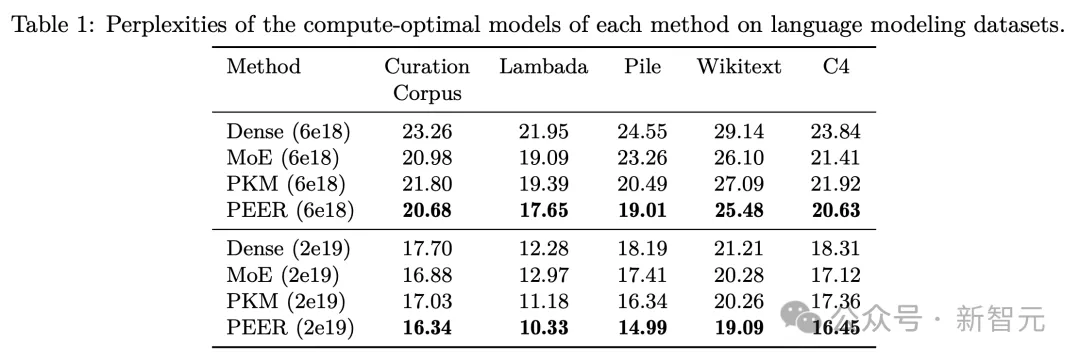
语言建模数据集评估
根据isoFLOP曲线确定每种方法的计算最优模型后，研究人员在几个流行的语言建模数据集上评估了这些预训练模型的性能，包括Curation Corpus、Lambada、the Pile、Wikitext和预训练数据集C4。评估结果如表1所示，作者根据模型在训练期间使用的FLOP预算将其分组。
消融实验
改变专家总数图1中isoFLOP图所示的模型都有超过一百万（10242）个专家。接下来，研究者进行了一项消融研究，研究专家数量N的影响，N决定了等式9中的总参数数量P。作者选择了isoFLOP最优模型，并改变PEER层中的专家数量（N = 1282, 2562, 5122, 10242），同时活跃专家的数量不变（h = 8, k = 16）。实验结果如图3(a)所示，可以看出，isoFLOP曲线在10242个专家的PEER模型和相应的密集骨干模型（未将中间块的FFW层替换为PEER层）之间进行插值。这表明，仅仅增加专家数量，就可以提高模型性能。
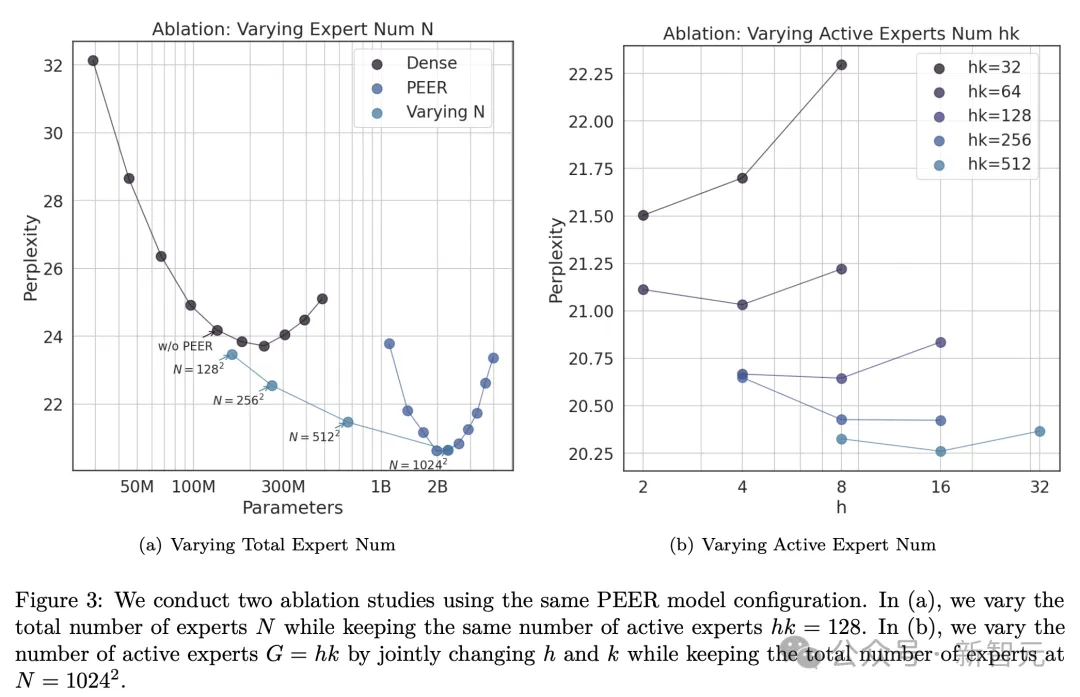改变活跃专家的数量另外，作者还对活跃专家hk数量进行了消融研究，hk等同于等式9中的粒度G。他系统地改变了活跃专家的数量（hk = 32, 64, 128, 256, 512），同时保持专家总数不变（N = 10242）。此外，对于给定的hk，同时改变h和k以找到最优组合。结果中的isoFLOP曲线，以头（h）数为横轴绘制，如图3（b）所示。结果表明，在考虑的数值范围内，更高的h·k值通常会带来更好的性能。值得注意的是，随着h·k的增加，最优的h也在增加。然而，性能逐渐趋于饱和，增加活跃专家的数量也会增加设备内存消耗，可能需要额外的加速器设备。因此，在实际应用中，应该根据性能、设备数量和计算资源需求之间的权衡来选择适当的h·k值。专家使用和查询批归一化由于PEER层中有超过一百万个专家，对于许多人来说，一定好奇其在推理过程中实际选择了多少专家？它们的使用是否均匀分布？为了分析这点，研究者在C4验证集的所有token中，为每个专家ei保留一个累积的路由分数（router score），表示为：
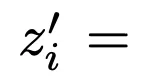
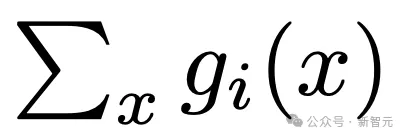
。其中，gi(x)是指当token x作为输入时用于聚合专家输出的路由分数。如果专家ei未被选中，则gi(x)=0。从这些累积的路由分数中，可以获得一个经验概率分布向量，表示为
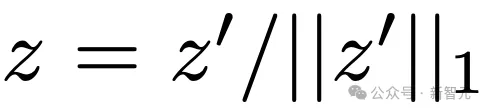
。代表C4验证集上所有专家的分布。然后，作者计算了Lample等人提出的以下指标来评估专家的使用情况和分布：- 专家使用：推理过程中检索到的专家比例：
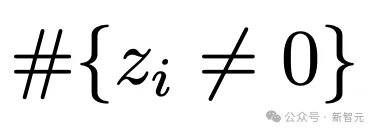
– 不均匀性：z与均匀分布之间的KL散度
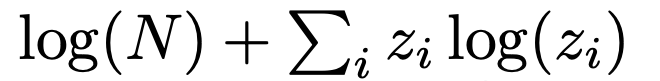
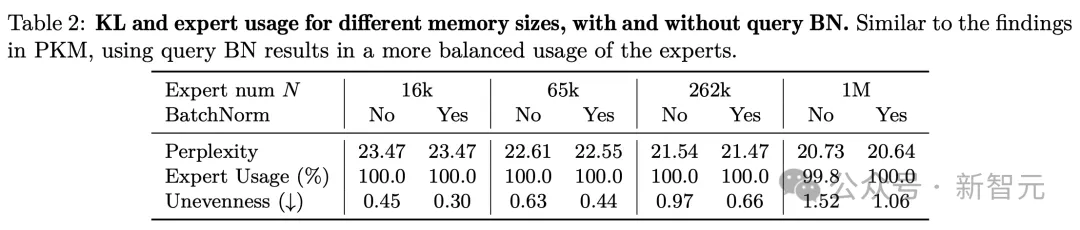
其中，N是专家总数。默认设置下，作者在查询网络上添加了一个批归一化（BN）层，目的是增加训练过程中的专家使用率。对此，他研究添加这个BN层对上述指标的影响。表2展示了不同专家数量下的专家使用和不均匀性，包括使用和不使用BN的情况。可以看到，即使对于100万个专家，专家使用率也接近100%，而使用BN可以导致专家的使用更加平衡，并降低困惑度。这些发现证明了，PEER模型在利用大量专家方面的有效性。
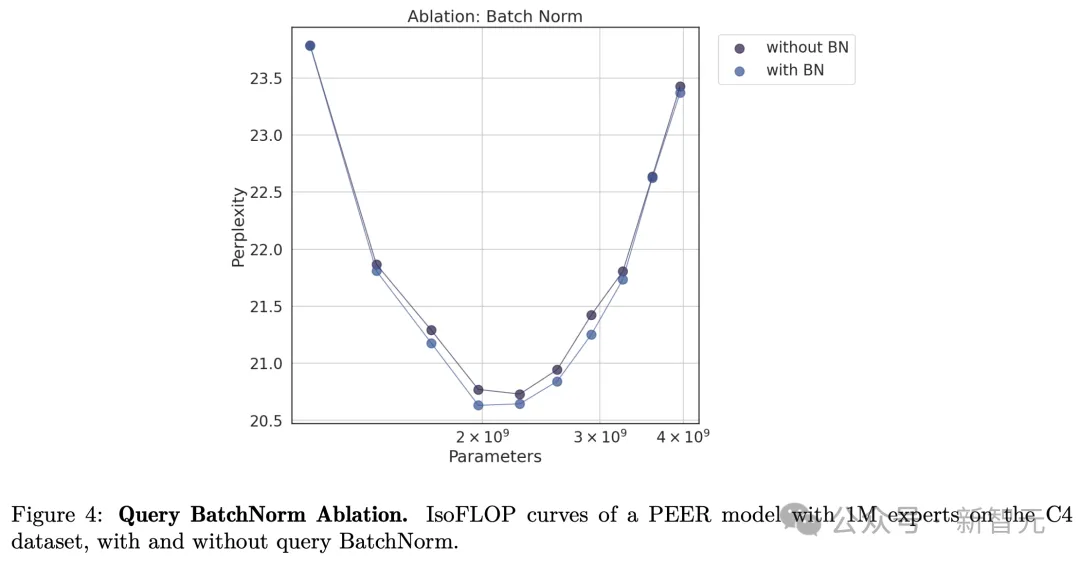
最后，作者还比较了有和没有批归一化（BN）的isoFLOP曲线。如下图4所示，使用BN的PEER模型通常能达到更低的困惑度。虽然差异不是很显著，但在isoFLOP最有区域附近最为明显。
作者介绍
Owen He是Google DeepMind的研究科学家，专注于持续学习和基础模型。在加入DeepMind之前，Owen是在格罗宁根大学和不来梅雅各布大学（康斯特大学）攻读博士学位，导师是 Herbert Jaeger。在此期间，Owen访问过Mila、马克斯·普朗克研究所、伯尔尼大学和苏黎世联邦理工学院，并在Google DeepMind进行过实习。他曾组织过ICML 2021持续学习研讨会，目前担任Conference on Lifelong Learning Agents的出版主席。
暂无评论内容