一觉醒来,超越Transformer和Mamba的新架构诞生了?

斯坦福、UCSD、UC伯克利和Meta的研究人员提出了一种全新架构,用机器学习模型取代RNN的隐藏状态。

论文地址:https://arxiv.org/abs/2407.04620
这个模型通过对输入token进行梯度下降来压缩上下文,这种方法被称为「测试时间训练层(Test-Time-Training layers,TTT)」。

TTT层直接替代了注意力机制,解锁了具有表现力记忆的线性复杂度架构,使我们能够在上下文中训练包含数百万(未来可能是数十亿)个token的LLM。
作者相信,这个研究了一年多的项目,将从根本上改变我们的语言模型方法。

而结果证明,TTT-Linear和TTT-MLP直接赶超或击败了最强的Transformer和Mamba!
作者之一的Xiaolong Wang惊喜地表示:不敢相信,我们真的做到了。

更令人兴奋的是,虽然目前TTT只应用于语言建模,但在未来,它也可以用在长视频上,可谓前景远大。
在将来,当我们对长视频进行建模时,就可以对帧进行密集采样,而不是采样1FPS了。这些密集帧对Transformer是一种负担,但对于TTT层来说,这却是一种福音!
一个5年多的想法,终于实现了
作者表示,在过去的1.5年里,团队一直在开发一种新的LLM架构,可以具有线性复杂度和更强的隐藏状态,用于长上下文建模。
而这个测试时训练(TTT)的想法,已经研究了超过5年。
Xiaolong清晰记得,在刚开始做博士后时,Alyosha曾让自己去找Yu Sun讨论TTT。
这次会面,就是这项研究的起点。

序列模型会把历史上下文存储在一个隐藏状态中。
像Mamba这样的RNN层,会随着时间的推移压缩成一个固定大小的状态,它们虽然效率很高,但性能受限于其表达能力。
注意力机制有一个KV缓存,它会随着时间的推移不断增长。这个状态不会压缩任何历史上下文,但随着上下文长度的增加,成本也会越来越高。
团队成员想:既然这样,为什么不把上下文压缩到模型的权重中——就像LLM处理互联网数据那样呢?
这种「隐藏状态模型」既能在时间上保持固定大小,又能大大增强表达能力。
研究人员使用了自监督学习来更新隐藏状态的权重,对每个token进行一次梯度下降。在处理一个序列时,该状态已经在其上下文窗口中的token上「训练」过了。
值得注意的是,隐藏状态只存在于端到端架构中的一层。其他组件,比如QKV投影矩阵,是在预训练期间通过标准的交叉熵目标函数学习的。
因此,端到端架构实际上是在进行元学习,寻找压缩上下文的最佳方式,以便更好地预测下一个token,也就是在「学习如何在测试时学习」。
结果显示,与Mamba相比,TTT-Linear具有更好的困惑度和更少的FLOP(左),并且更好地利用了长上下文(右)。
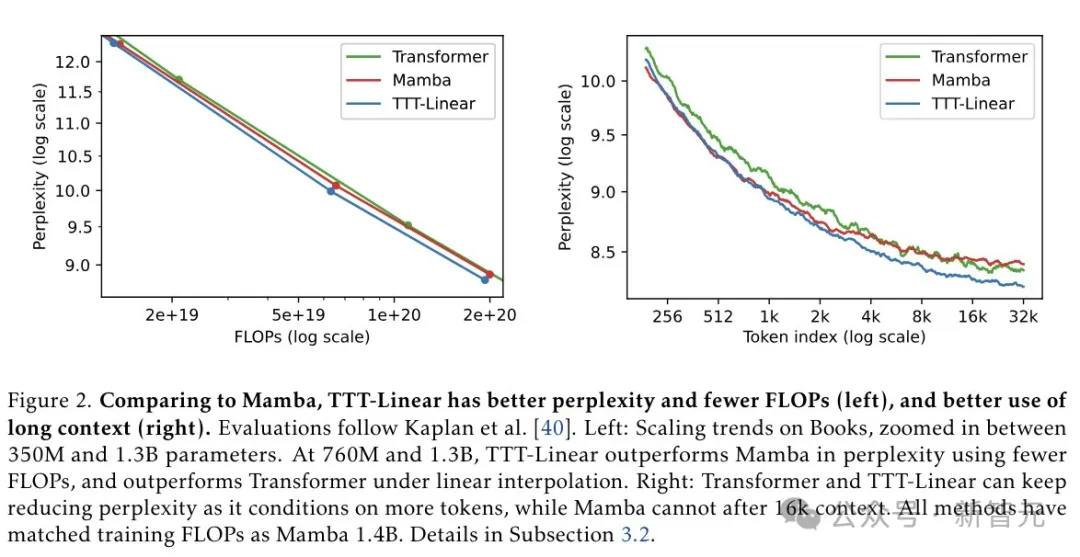
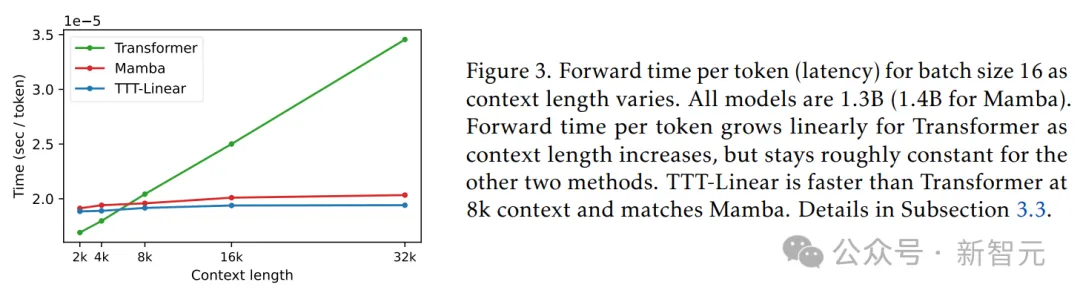
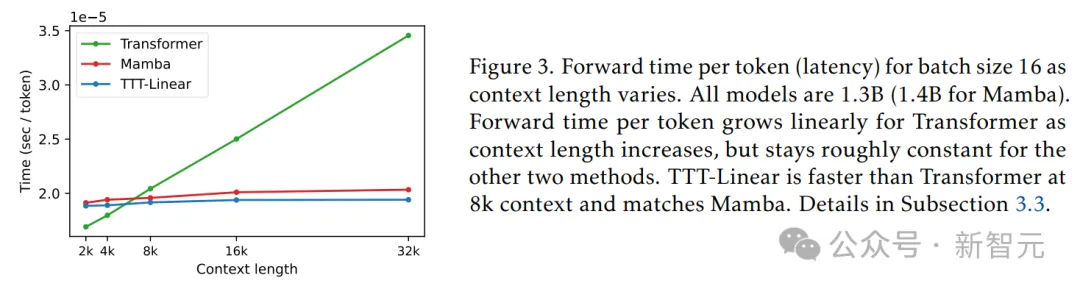
下图显示了批大小为16的情况下,随着上下文长度的变化,每个token的前向时间(延迟)。所有模型的参数都是1.3B(Mamba为1.4B)。
可以看到,随着上下文长度的增加,Transformer每个token的前向时间呈线性增长,但其他两种方法的前向时间基本保持不变。
在8k上下文时,TTT-Linear比Transformer更快,与Mamba相当。
RNN的尴尬现实
2020年,OpenAI缩放定律论文表明LSTM(RNN的一种)无法像Transformer那样进行缩放,或有效地使用长上下文。
真的是这样吗?
在这个项目中,研究人员重新评估了图2中的这些发现。
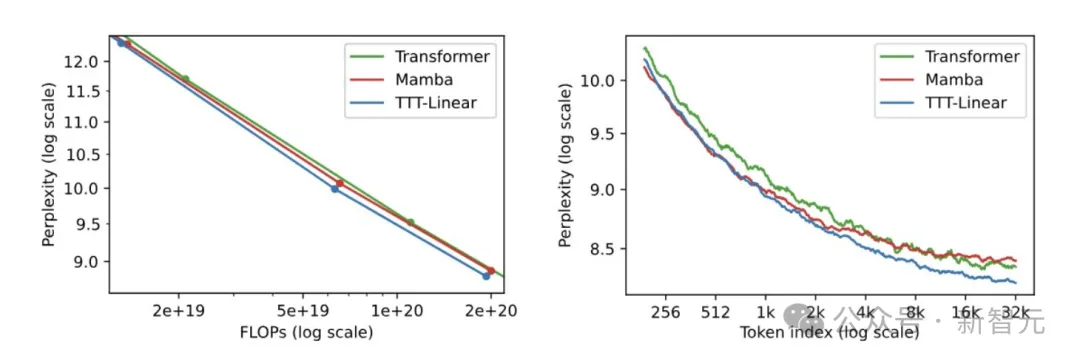
在左侧,可以观察到Mamba(当今最流行的RNN之一)的扩展性与强大的Transformer类似,这是自2020年的LSTM以来显示出的巨大进步。
然而,在右侧,可以观察到与OpenAI相同的Mamba问题。
平均而言,序列中靠后的token应该更容易预测,因为它们以更多信息为条件。
对Transformer来说确实如此,每个token索引的平均复杂度在其32k上下文中不断减少。相比之下,Mamba在16k后就出现了同样的情况。
对于现有的RNN来说,这个结果代表了一个尴尬的现实——
一方面,RNN(相对于Transformer)的主要优势就是它们的线性(相对于二次)复杂性。这种渐进优势实际上只会在长上下文中实现。
另一方面,一旦上下文足够长,现有的RNN(如Mamba)就很难真正利用额外的条件信息。
长上下文的困难是RNN层本质上的问题:与自注意力机制不同,RNN层必须将上下文压缩为固定大小的隐藏状态。
作为一种压缩启发式,更新规则需要发现成千上万甚至数百万个token之间的底层结构和关系。
研究人员首先观察到,自监督学习可以将大量训练集压缩为LLM等模型的权重,该模型通常表现出对其训练数据之间语义联系的深刻理解,而这,恰恰是他们所需要的。

TTT层
受此启发,研究人员设计了一类新的序列建模层,其中隐藏状态是模型,更新规则是自监督学习的一个步骤。
由于更新测试序列上隐藏状态的过程,相当于在测试时训练模型,因此此类新层称为测试时训练(TTT)层。
研究人员引入两个简单的实例:TTT-Linear和TTT-MLP,其中隐藏状态分别是线性模型和两层MLP。TTT层可以集成到任何网络架构中并进行端到端优化,类似于RNN层和自注意力。
实际运行时间
TTT层在FLOP方面已经非常高效,研究人员则更进一步地提出了两项创新,使其在实际运行时间内也能保持高效。
首先,与在常规训练中对mini-batch序列采取梯度步进以实现更好的并行性类似,他们也在TTT中使用了mini-batch的token。
其次,研究人员为每个TTT mini-batch内的操作开发了一种对偶形式,以更好地利用现代GPU和TPU。这种对偶形式的输出与原始实现相当,但训练速度却快了5倍以上。
正如图3所示,TTT-Linear在8k上下文中比Transformer更快,并且与Mamba相当。
Transformer杀手——TTT
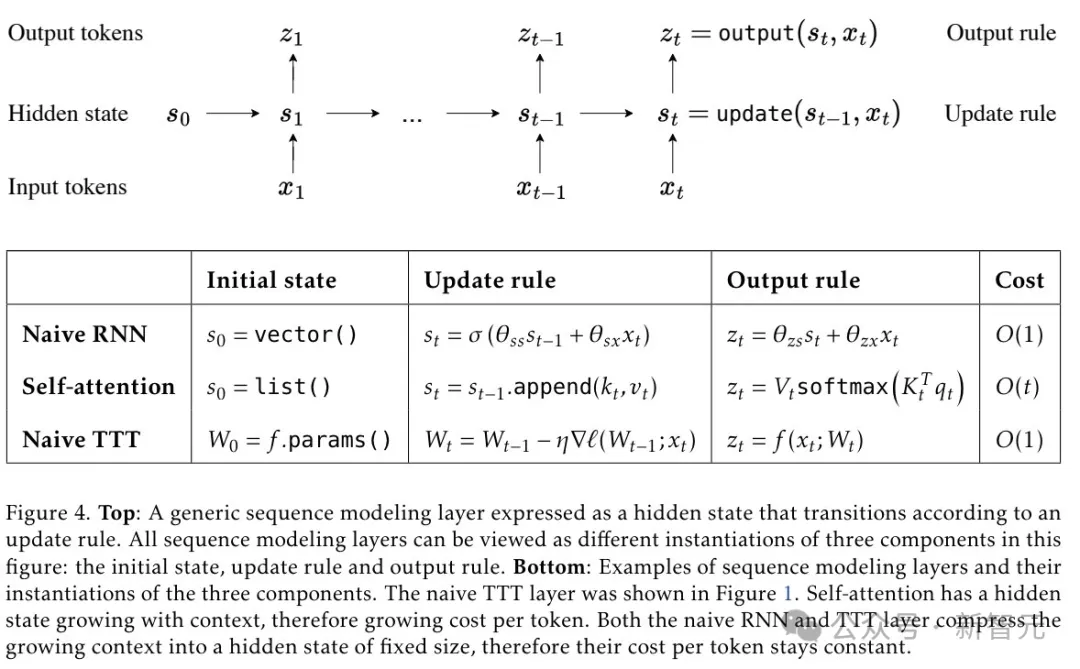
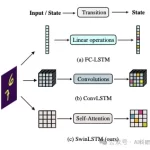
如图4所示,所有的序列建模层,都可以从将历史上下文存储到隐藏状态的角度来看待。
比如,RNN层——如LSTM、RWKV和Mamba层——将上下文压缩成一个固定大小的状态,这个状态随时间变化。
这种压缩带来了两种结果:优势是处理效率高,因为每个token的处理时间是恒定的。劣势是在处理长上下文时,RNN性能受限于隐藏状态的「表达能力」。
自注意力机制(Self-attention)也可以从如上角度来理解。
不同之处在于,它的隐藏状态,通常称为键值(KV)缓存是一个随t增长的线性list。
它可以存储所有的上下文,并且不会进行压缩,具有很好的表达能力,不过其处理时间随上下文长度线性增长。

因此,为了在长上下文中既保持效率,又具有表达能力,需要一个更好的「压缩启发式」(compression heuristic)方法。
具体来说,就需要将数百万个token压缩成一个能有效捕捉其底层结构和关系的隐藏状态。
TTT隐藏状态
研究人员的关键思想是,使用自监督学习来将历史上下文

压缩成一个隐藏状态
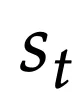
。
方法是将上下文视为一个无标签数据集,而将状态视为一个模型。
具体来说,隐藏状态
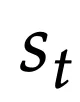
现在等同于一个模型f的权重
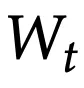
,这个模型f可以是线性模型、小型神经网络或其他任何形式。输出规则简单地表示为:

直观讲,输出token就是由更新后权重
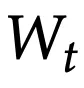
的模型f对

所做的预测。更新规则是在某个自监督损失ℓ上进行的一步梯度下降:

其中学习率为η。从压缩的角度来看,每种启发式方法都需要决定记住/忘记哪些输入。W会记住那些产生大梯度的输入——直观地说,就是那些使W学习很多的输入。
ℓ的一种选择是重构
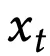
本身。为了使学习问题变得非平凡,作则首先将
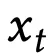
处理成一个被破坏的输入
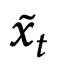
,然后优化:

类似于去噪自编码器,f需要发现
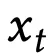
各维度之间的相关性,以便从部分信息
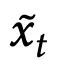
中重构出
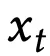
。
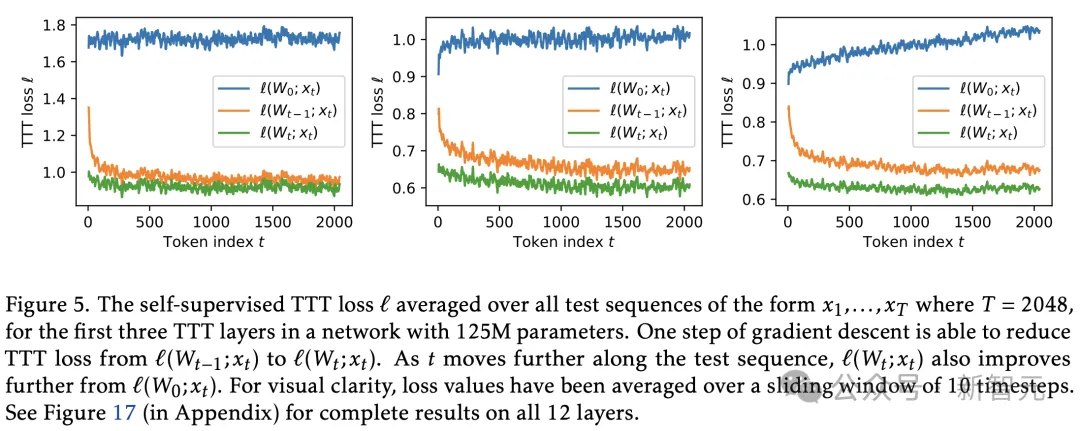
如图5所示,梯度下降能够减少ℓ,但无法将其降至零。
与其他RNN层和自注意力机制一样,研究人员将输入序列

映射到输出序列
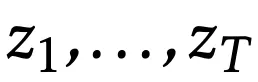
的算法可以被编程到序列建模层的前向传播中,使用上述的隐藏状态、更新规则和输出规则。
即使在测试时,新层仍然为每个输入序列训练一个不同的权重序列

。
因此,研究人员将其称之为测试-时间训练层(TTT)。
使用TTT层训练神经网络
TTT层的前向传播,也有相应的后向传播。
TTT层与RNN层、自注意力机制有着相同的接口,因此可以在任何更大的神经网络架构中替换它们。
值得一提的是,训练带有TTT层神经网络的方式,与训练任何其他Transformer模型相同。
可以使用相同的数据、方法和目标(如下一个token预测)来优化网络其余部分的参数。
在此,研究人员将训练更大的神经网络称为外循环(outer loop),而在每个TTT层内训练W称为内循环(inner loop)。
它们之间梯度计算的区别是,内循环针对的是W(即模型f的参数),外循环针对的是网络其余部分的参数
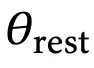
。
TTT学习自监督任务
可以说,TTT最重要的部分是自监督任务,因为它决定了W从测试序列中学习的特征类型。
在这个任务的设计上,研究人员采取了更加端到端的方法——直接优化自监督任务以实现下一个token预测的最终目标。
具体来说,研究着将自监督任务的学习,作为外循环的一部分。
从如上公式3中的简单重构任务开始,添加了一些外循环参数来让这个任务可学习。最新的自监督损失是:
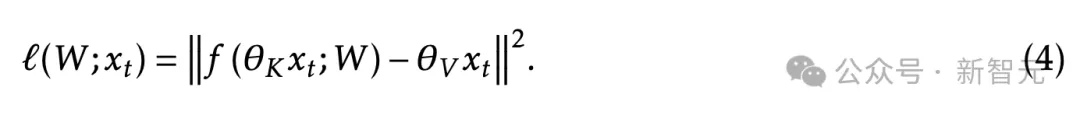
在内循环中,只有W被优化,因此作为ℓ的参数写出;θ们是这个损失函数的「超参数」。在外循环中,
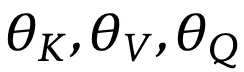
与
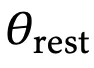
一起被优化,而W仅仅是一个隐藏状态,不是参数。
图6用代码说明了这种区别,其中
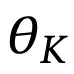
和
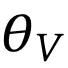
被实现为TTT层的参数,类似于自注意力中的KV参数。

总的来说,
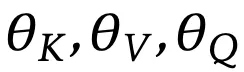
所有可能的选择构成了一系列多视图重构任务,外循环可以被理解为从这个任务组中选择一个具体任务。为了简单起见,研究人员在这里将所有视图设计为线性投影。
mini-batch TTT并行化
目前,开发的原生TTT层在浮点运算(FLOP)次数方面已经非常高效。
然而,其更新规则
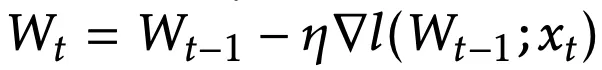
无法实现并行化,因为
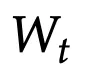
在两个位置上依赖于
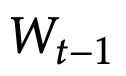
:负号和
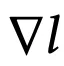
。
对此,研究人员提出了mini-batch梯度下降,用b表示TTT批大小。
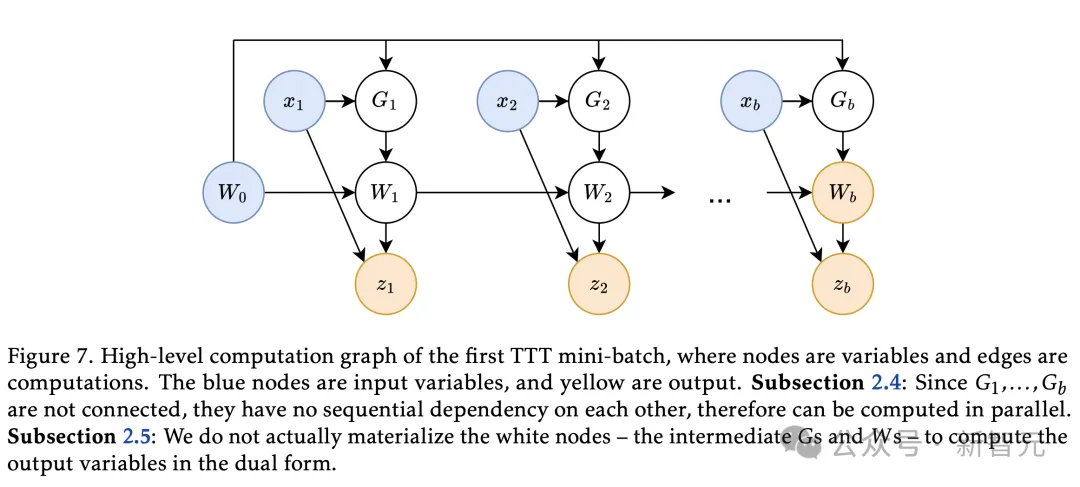
研究中使用
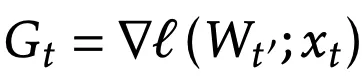
,其中

代表着前一个mini-batch的最后一个时间步(或者第一个mini-batch 0),因此,可以一次并行b个梯度计算。
对偶形式
上面介绍的并行化是必要的,但对于「实际运行时间」(wall-clock time)的效率来说还不够。
正如之前所述,可以对于t = 1, . . . , b进行并行计算:
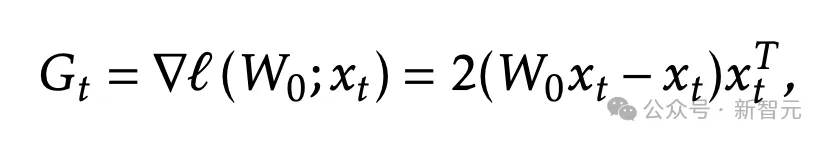
然而,现实中,是无法对单个matmul来计算
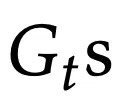
所有的b。
相反,需要b个外积来对其进行一一计算。更糟糕的是,对于每个

,
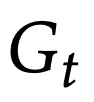
是d×d,这会比大d
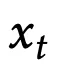
产生更大的内存占用和I/O成本。
为了解决这两个问题,研究人员观察到:我们实际上并不需要具体化G1, . . . , Gb,只要要我们可以在mini-batch结束时计算
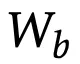
,并且输出token z1, . . . , zb(如上图7所示)。
现在,就可以用上面简化的TTT-Linear情况来演示这些计算,表示X = [x1, . . . , xb]:
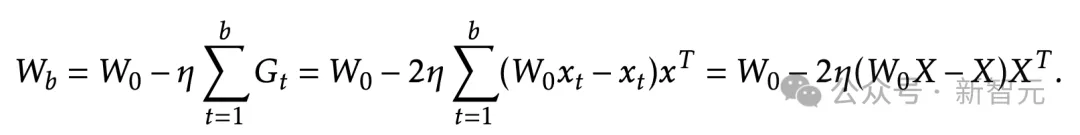
所以
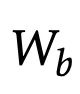
可以用matmul方便地计算出来。为了计算Z = [z1, . . . , zb],我们知道:
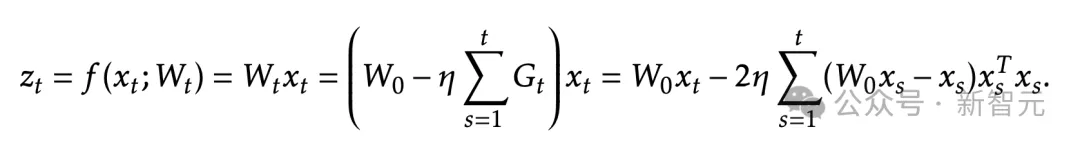
表示
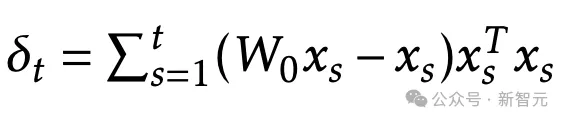
和矩阵
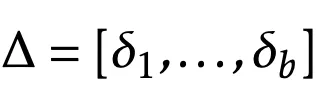
,可以得出:
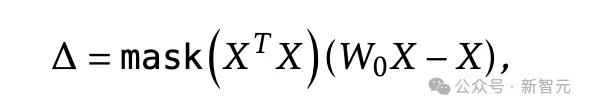
如上过程,研究人员将其称为「对偶形式」。
理论等价
前面已经提到f可以是线性模型,也可以是神经网络。还有更新规则的三种变体:online GD、batch GD和mini-batch GD。
如下图所示,在这些2×3组合中,每一种都会引起TTT层的不同实例化。
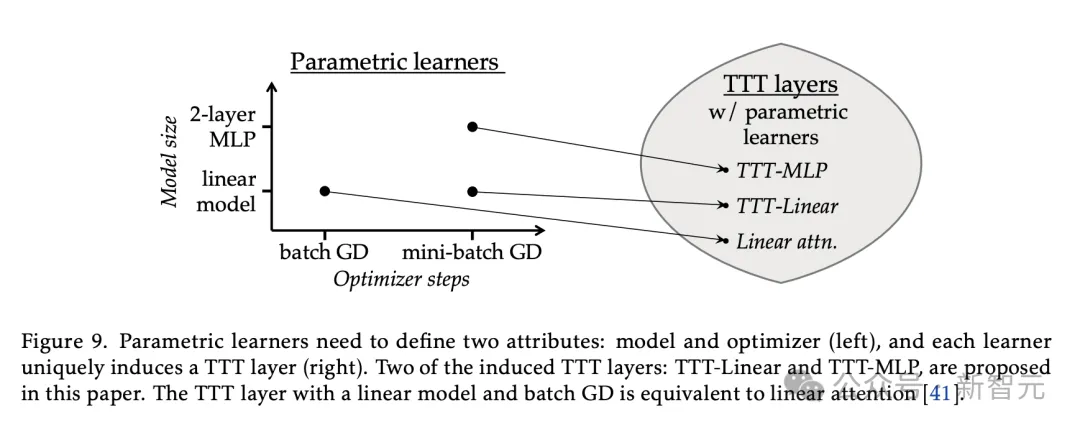
研究中,作者分别从2个定理证明了在这些诱导实例中,具有线性模型和batch GD的TTT层等同于线性注意力——一个广为人知的RNN层。
图10总结了所有序列建模层的更广泛范围内TTT层的一般定义。
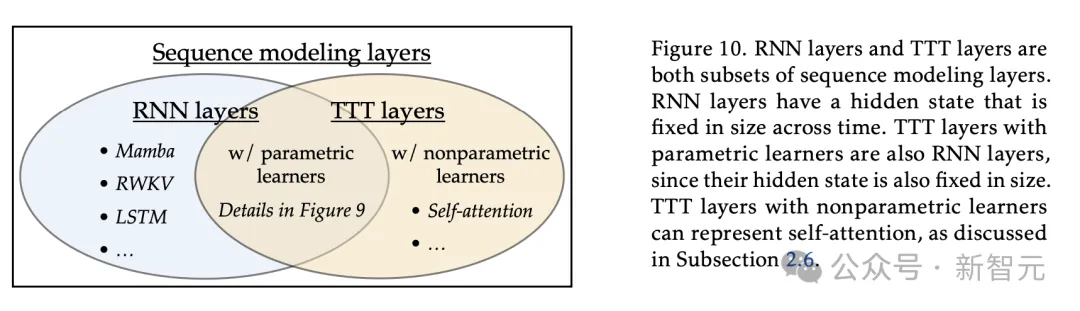
两种变体
研究中,作者提出了TTT层的两种变体TTT-Linear和TTT-MLP,仅在f的实例化方面有所不同。
对于TTT-Linear,
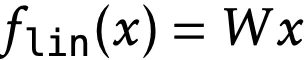
,其中W是平方。对于TTT-MLP,

有两层,类似于Transfomer的MLP。
具体来说,隐藏维度是4×输入维度,然后是GELU激活。为了在TTT期间获得更好的稳定性,f始终包含层归一化 (LN) 和残差连接。
即,
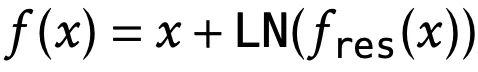
,其中,

可以是
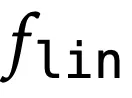
或

。
实验
通过与两个基线Transformer和Mamba(现代RNN)比较,研究人员评估了TTT-Linear和TTT-MLP。
数据集
继续Mamba论文之后,研究人员在Pile上执行了2k和8k上下文长度的标准实验,Pile是一个用于训练开源LLM的流行文档数据集。
主架构
Transformer和Mamba使用不同的,除非另有说明,TTT-Linear和TTT-MLP始终使用Mamba架构。
短上下文:the Pile
在2k上下文中,TTT-Linear(M)、Mamba和Transformer具有相当的性能,线条大部分重叠。
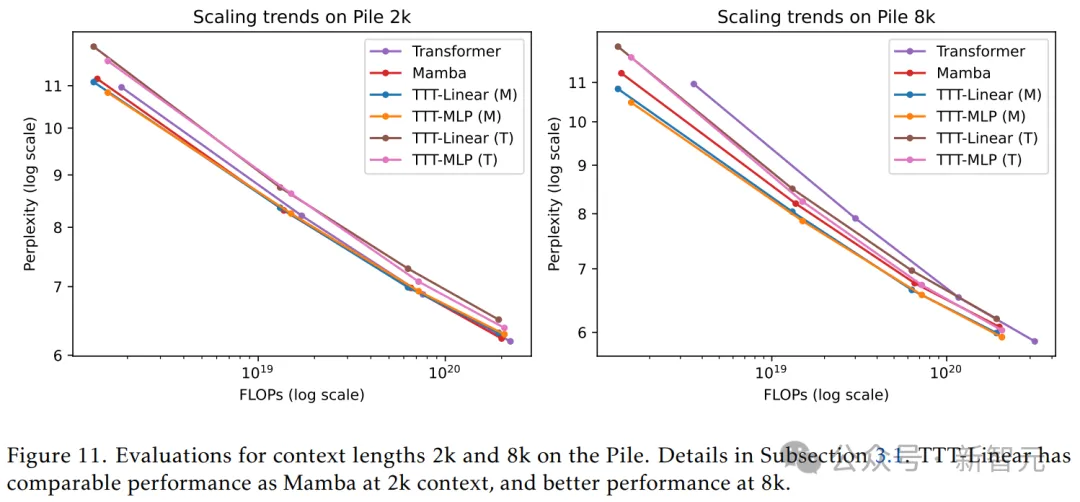
TTT-MLP(M)在较大的FLOP预算下表现稍差。尽管TTT-MLP在每个模型大小上,都比TTT-Linear具有更好的复杂度,但FLOP的额外成本抵消了这种优势。
在8k上下文中,TTT-Linear(M)和TTT-MLP(M)的表现均明显优于Mamba。即使是具有Transformer架构的TTT-MLP(T),性能也比Mamba略好。
另外,研究人员还观察到了一个非常明显的现象:随着上下文长度变长,TTT层相对于Mamba的优势就更大了。
长上下文:Books
为了评估长上下文中的功能,研究人员使用了Pile的一个流行子集——Books,对从1k到32k以2个增量的上下文长度进行了实验。
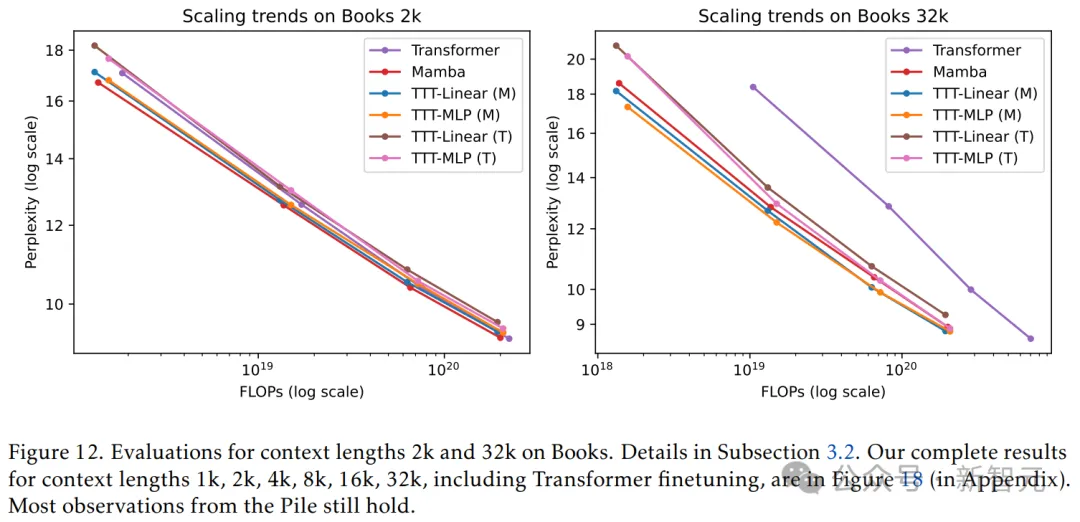
根据上图,可以观察到——
在Books的2k上下文中,Pile 2k的所有观察结果仍然成立,唯一的例外是Mamba的表现略好于TTT-Linear。
在32k上下文中,TTT-Linear(M)和TTT-MLP(M)的性能均优于Mamba,与Pile 8k的观察结果类似。即使具有Transformer架构的TTT-MLP(T),在32k上下文中的表现也比Mamba稍好。
在1.3B尺度上,TTT-MLP(T)仅比TTT-MLP(M)稍差。由于缺之清晰的线性拟合,很难推导出经验缩放定律。然而,TTT-MLP(T)的强劲趋势表明,Transformer架构可能更适合超出评估的更大模型和更长上下文。
上下文长度作为超参数
虽然输入序列的长度由用户确定,但语言模型处理输入的上下文长度可以由工程师确定。因此,上下文长度也是一个可以选择的超参数。
对于具有线性复杂度的LLM,研究人员选择了困惑度中的argmin,因为每个上下文长度都有相同的FLOP。
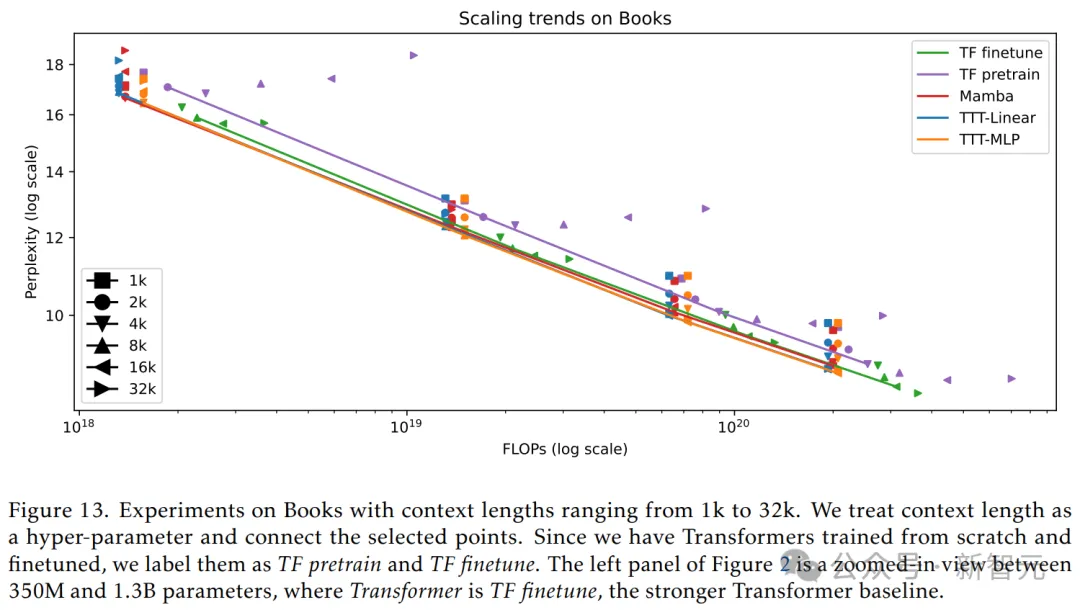
从图13中,可以观察到以下结果——
– 性能最好的方法TTT-Linear和TTT-MLP的线几乎完全重叠。Mamba和TF Finetune的线在10^20 FLOP后也大部分重叠。
– TF Finetune的性能明显优于TF Pretrain,因为它受益于长上下文,而不会在训练FLOP中产生极大的成本。
– 对于所有从头开始训练的方法(包括TF预训练),一旦上下文长度变得太大,困惑度就会变得更糟。
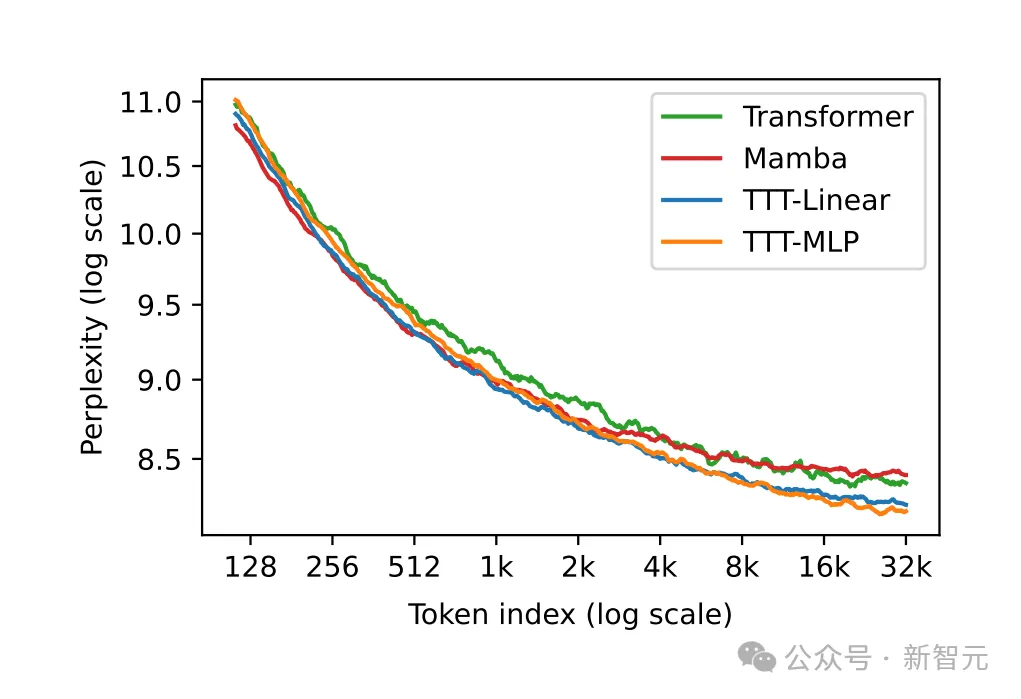
从上图可见,与TTT-Linear相比,TTT-MLP在短上下文中表现稍差,但在长上下文中表现更好。
这一观察结果正符合研究人员的预期,即作为隐藏状态的MLP比线性模型更具表现力。同样,所有方法都具有与Mamba 1.4B相同的训练FLOP。
实际运行时间
LLM训练和推理可以分解为前向、后向和生成。
由于前向(在训练和推理期间)和后向都可以并行化,因此研究人员使用对偶形式。生成新token(也称为解码)本质上是顺序的,因此研究人员使用原始形式。
由于资源限制,这项实验是用JAX编写并在TPU上运行的。
然而,由于Mamba(在PyTorch、Triton和CUDA中实现)只能在GPU上运行,因此为了公平比较,研究人员还重写了方法,以在GPU上运行。
具体来说,研究人员在ThunderKittens中编写了一个用于前向的GPU内核。从历史上看,由于并行性和矩阵相乘的使用不当,RNN在前向和后向过程中效率低下。
这个前向内核的目标,是证明mini-batch TTT和这些问题对偶形式的有效性。
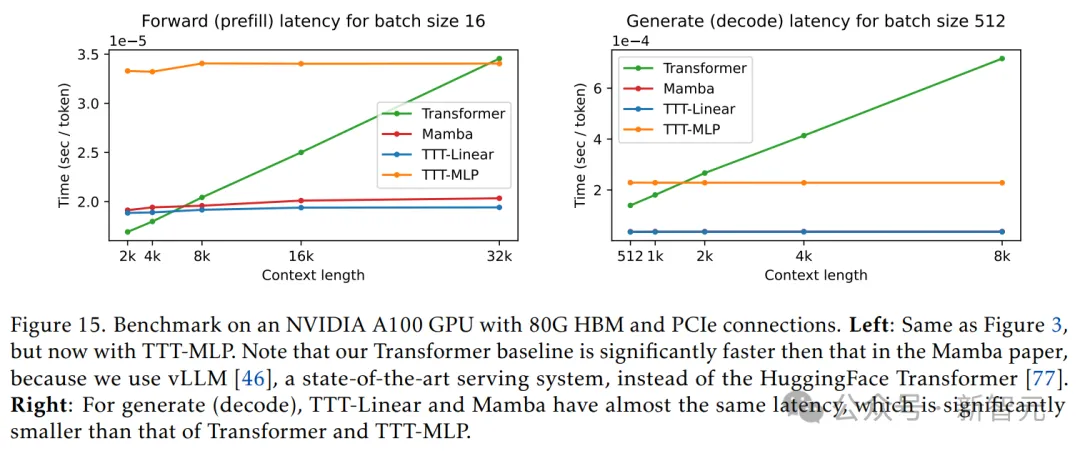
图15的左图显示了前向内核批大小为16的延迟。所有模型参数均为1.3B(Mamba为 1.4B)。
对于Transformer,每个token的时间随着上下文长度的增加而线性增长,但对于其他方法则大致保持不变。
此外,研究人员在Triton中编写了另一个用于生成的GPU内核,并在图15的右图中对批大小为512的速度进行了基准测试。
可以看出,TTT-Linear和Mamba的延迟几乎相同,明显小于Transformer和TTT-MLP。
Mamba之后,又看到TTT这么能打的新架构诞生,少不了AI社区的热议。
有网友称,这会不会是最接近实时上下文的方法?很想听听大家的想法。这意味着TTT甚至在使用过程中,也能够学习和适应,为长上下文提供更好的性能,而不会产生通常与Transformer相关的高昂计算成本。

OpenAI视频生成研究人员对此表示,这项研究看起来很有趣。

如果scaling law依然存在,TTT将带来难以置信的影响。对于长序列,Transformer的计算成本往往很高,当长序列变得更长时,RNN会遗忘。TTT训练巧妙地利用神经网络解决RNN的不足。

作者介绍
论文最后,分别列出了这篇研究的作者贡献。

其中的核心作者是,Yu Sun、Xinhao Li和Karan Dalal。
Yu Sun

Yu Sun是斯坦福大学计算机专业的博士后,导师是Carlos Guestrin、Tatsu Hashimoto和Sanmi Koyejo。
此前,他曾在加州大学伯克利分校完成了电子工程科学博士学位,导师是Alyosha Efros和Moritz Hardt。他还在康奈尔大学拿到了学士学位。
个人主页中,他介绍自己的研究重点是一种名为测试时间训练(test-time training)的算法框架。其核心思想是,每个测试实例都定义了自己的学习问题,都有自己的泛化目标。这通常使用自监督学习,为每个实例即时训练一个不同的模型来实现的。
在最新研究中,Yu Sun与Xinhao Li在2022年11月共同启动了这一项目。自2023年6月起,Yu Sun专职负责该项目。
他提出了项目的概念框架,设计了mini-batch TTT和对偶形式(dual form)。
Xinhao Li

Xinhao Li是UC San Diego研二的学生,导师是Xiaolong Wang教授。他本人的研究兴趣主要是深度学习和计算机视觉。
他在斯坦福大学Tatsunori Hashimoto教授的团队中作为访问学生,与Yu Sun博士和其他导师朋友一起工作。在此之前,他曾在电子科技大学获得了学士学位。
在2024年3月之前,Xinhao Li是TTT早期代码库的主要贡献者,这些代码库塑造了最新项目。
Karan Dalal

Karan Dalal是UC Berkeley电子工程科学系的本科生。他于2023年6月全职加入该项目,与Xinhao Li合作共同领导了当前代码库的开发工作。









暂无评论内容